题目内容
 已知定义在区间[-π,
已知定义在区间[-π,| 2 |
| 3 |
| π |
| 6 |
| 2 |
| 3 |
| π |
| 2 |
| π |
| 2 |
(1)求函数y=f(x)在[-π,
| 2 |
| 3 |
(2)求方程f(x)=
| ||
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的求值,三角函数的图像与性质
分析:(1)首先求出函数在[-
,
]上的解析式,然后设-π≤x<-
,求出-
≤-x-
≤
,结合函数y=f(x)的图象关于直线x=-
对称求得答案;
(2)由-
≤x≤
得到
≤x+
≤π,再由f(x)=sin(x+
)=
求得x的值.-π≤x<-
直接带入函数解析式求得x的值.
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
(2)由-
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| π |
| 6 |
解答:
解:(1)当x∈[-
,
]时,A=1,
=
-
,T=2π,ω=1.
且f(x)=sin(x+φ)过点(
,0),
则
+φ=π,φ=
.
f(x)=sin(x+
).
当-π≤x<-
时,-
≤-x-
≤
,
f(-x-
)=sin(-x-
+
),
而函数y=f(x)的图象关于直线x=-
对称,
则f(x)=f(-x-
),
即f(x)=sin(-x-
+
)=-sinx,-π≤x<-
.
∴f(x)=
;
(2)当-
≤x≤
时,
≤x+
≤π,
由f(x)=sin(x+
)=
,
得x+
=
或
,x=-
或
.
当-π≤x<-
时,由f(x)=-sinx=
,即sinx=-
,
得x=-
或-
.
∴x=-
或-
或-
或
.
| π |
| 6 |
| 2π |
| 3 |
| T |
| 4 |
| 2π |
| 3 |
| π |
| 6 |
且f(x)=sin(x+φ)过点(
| 2π |
| 3 |
则
| 2π |
| 3 |
| π |
| 3 |
f(x)=sin(x+
| π |
| 3 |
当-π≤x<-
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
f(-x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
而函数y=f(x)的图象关于直线x=-
| π |
| 6 |
则f(x)=f(-x-
| π |
| 3 |
即f(x)=sin(-x-
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
∴f(x)=
|
(2)当-
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
由f(x)=sin(x+
| π |
| 3 |
| ||
| 2 |
得x+
| π |
| 3 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 12 |
| 5π |
| 12 |
当-π≤x<-
| π |
| 6 |
| ||
| 2 |
| ||
| 2 |
得x=-
| π |
| 4 |
| 3π |
| 4 |
∴x=-
| π |
| 4 |
| 3π |
| 4 |
| π |
| 12 |
| 5π |
| 12 |
点评:本题考查了由y=Asin(ωx+φ)的部分图象求函数解析式,考查了分类讨论的数学思想方法,训练了三角函数值的求法,是中档题.

练习册系列答案
相关题目
将2个数a=1,b=3交换,使a=3,b=1,下面语句正确的一组是( )
| A、a=b,b=a |
| B、c=b,b=a,a=c |
| C、b=a,a=b |
| D、a=c,c=b,b=a |
若集合A={x||x-3|<2},B={x|x≥3},那么A∩B=( )
| A、(1,3] |
| B、[3,5) |
| C、(3,+∞] |
| D、[3,5] |
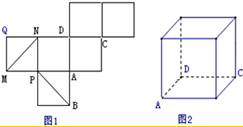 图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题
图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题