题目内容
7.将函数f(x)=sin2x的图象向右平移φ$({0<φ<\frac{π}{2}})$个单位后得到函数g(x)的图象,若g(x)在区间$[{0,\frac{π}{6}}]$上单调递增,且函数g(x)的最大负零点在区间$({-\frac{π}{3},-\frac{π}{6}})$上,则φ的取值范围是( )| A. | [$\frac{π}{12}$,$\frac{π}{4}$] | B. | [$\frac{π}{6}$,$\frac{5π}{12}$) | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | ($\frac{π}{6}$,$\frac{π}{4}$] |
分析 利用函数f(x)=sin2x的图象平移后的图象位置特征,列出关于φ的关系式.
解答 解:将函数f(x)=sin2x的图象向右平移φ$({0<φ<\frac{π}{2}})$个单位后得到函数g(x)的图象,
而f(x)=sin2x的图象如下图:
f(x)=sin2x的单调增区间为[-$\frac{π}{4}$+kπ,$\frac{π}{4}$+kπ],零点x=$\frac{kπ}{2}$,
①g(x)在区间$[{0,\frac{π}{6}}]$上单调递增,则有:
$\left\{\begin{array}{l}{-\frac{π}{4}+φ≤0}\\{\frac{π}{4}+φ≥\frac{π}{6}}\end{array}\right.$;
得$\frac{π}{12}$≤φ≤$\frac{π}{4}$,
②函数g(x)的最大负零点在区间$({-\frac{π}{3},-\frac{π}{6}})$上,则有:
-$\frac{π}{2}$+φ∈$({-\frac{π}{3},-\frac{π}{6}})$,
得$\frac{π}{6}$<φ<$\frac{π}{3}$,
综上,$\frac{π}{6}$<φ≤$\frac{π}{4}$.
选D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的单调性和零点,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
19.设F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的右焦点,若OF的垂直平分线与渐近线在第一象限内的交点到另一条渐近线的距离为$\frac{1}{2}|OF|$,则双曲线的离心率为( )
| A. | $2\sqrt{2}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $2\sqrt{3}$ | D. | 3 |
12.已知$\overrightarrow{OA}=(1,1,0)$,$\overrightarrow{OB}=(4,1,0)$,$\overrightarrow{OC}=(4,5,-1)$,则向量$\overrightarrow{AB}$和$\overrightarrow{AC}$的夹角的余弦值为( )
| A. | $\frac{{\sqrt{26}}}{26}$ | B. | $\frac{{\sqrt{26}}}{12}$ | C. | $\frac{{3\sqrt{26}}}{26}$ | D. | $\frac{{2\sqrt{26}}}{13}$ |
16.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0,则( )
| A. | f(-3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(-3) | C. | f(-2)<f(1)<f(-3) | D. | f(-3)<f(1)<f(-2) |
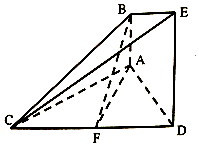 如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.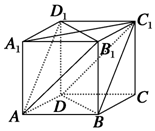 在正方体ABCD-A1B1C1D1中,如图.
在正方体ABCD-A1B1C1D1中,如图. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以原点为圆心,椭圆C的短半轴长为半径的圆与直线 x+y+$\sqrt{2}$=0相切.A、B是椭圆的左右顶点,直线l 过B点且与x轴垂直,如图.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以原点为圆心,椭圆C的短半轴长为半径的圆与直线 x+y+$\sqrt{2}$=0相切.A、B是椭圆的左右顶点,直线l 过B点且与x轴垂直,如图.