题目内容
已知数列{an}的每项均为正数,首项a1=1.记数列{an}前n项和为Sn,满足a13+a23+…+an3=Sn2.
(1)求a2的值及数列{an}的通项公式;
(2)若bn=
,记数列{bn}前n项和为Tn,求证:Tn<
.
(1)求a2的值及数列{an}的通项公式;
(2)若bn=
| 1 |
| an•an+3 |
| 11 |
| 18 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(1)由已知当n=2时,1+a23=(1+a2)2,解得a2=2.an+12=2(a1+a2+…+an)+an+1,从而an+1-an=1,进而数列{an}的首项为1,公差为1的等差数列,由此求出an=n.
(2)由
=
=
(
-
),利用裂项求和法能证明Tn<
.
(2)由
| 1 |
| an•an+3 |
| 1 |
| n(n+3) |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+3 |
| 11 |
| 18 |
解答:
解:(1)∵a1=1,a13+a23+…+an3=Sn2,
∴当n=2时,1+a23=(1+a2)2,解得a2=2.
由于a13+a23+…+an3=(a1+a2+…+an)2①
a13+a23+…+an3+an+13=(a1+a2+…+an+an+1)2②
②-①得an+13=(a1+a2+…+an+an+1)2-(a1+a2+…+an)2,
∵an>0,∴an+12=2(a1+a2+…+an)+an+1③,
同样有an2=2(a1+a2+…+an-1)+an(n≥2),④.
③-④an+12-an2=an+1+an,
∴an+1-an=1,∵a2-a1=1,即当n≥1时都有:an+1-an=1,
∴数列{an}的首项为1,公差为1的等差数列.故an=n.(7分)
(2)由(1)知an=n,则
=
=
(
-
),
∴Tn=
+
+
+…+
=
(
+
+
+…+
)=
(1-
+
-
+…+
-
)
=
(1+
+
-
-
-
)<
,
∴Tn<
.(14分)
∴当n=2时,1+a23=(1+a2)2,解得a2=2.
由于a13+a23+…+an3=(a1+a2+…+an)2①
a13+a23+…+an3+an+13=(a1+a2+…+an+an+1)2②
②-①得an+13=(a1+a2+…+an+an+1)2-(a1+a2+…+an)2,
∵an>0,∴an+12=2(a1+a2+…+an)+an+1③,
同样有an2=2(a1+a2+…+an-1)+an(n≥2),④.
③-④an+12-an2=an+1+an,
∴an+1-an=1,∵a2-a1=1,即当n≥1时都有:an+1-an=1,
∴数列{an}的首项为1,公差为1的等差数列.故an=n.(7分)
(2)由(1)知an=n,则
| 1 |
| an•an+3 |
| 1 |
| n(n+3) |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+3 |
∴Tn=
| 1 |
| a1a4 |
| 1 |
| a2a5 |
| 1 |
| a3a6 |
| 1 |
| anan+3 |
| 1 |
| 3 |
| 1 |
| 1•4 |
| 1 |
| 2•5 |
| 1 |
| 3•6 |
| 1 |
| n(n+3) |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| n |
| 1 |
| n+3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 11 |
| 18 |
∴Tn<
| 11 |
| 18 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
设集合A={-1,0,1},B={x|x2-x<2},则集合A∩B=( )
| A、{-1,0,1} |
| B、{-1,0} |
| C、{0,1} |
| D、{-1,1} |
三次函数f(x)=x3+bx2+cx+d(b,c,d∈R)在区间[-1,2]上是减函数,那么b+c的取值范围是( )
A、(-∞,
| ||
B、(-∞, -
| ||
| C、A(x0,f(x0)) | ||
D、(-∞,-
|
已知F1,F2为双曲线C:
-y2=1的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=( )
| x | 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
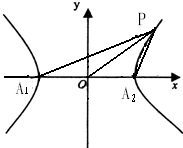 如图,P是双曲线
如图,P是双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||
B、(0,
| ||
C、(0,
| ||
D、(0,
|
已知A,B是两个相互独立事件,P(A),P(B)分别表示它们发生的概率,则1-P(A)P(B)是下列哪个事件的概率( )
| A、事件A,B同时发生 |
| B、事件A,B至少有一个发生 |
| C、事件A,B至多有一个发生 |
| D、事件A,B都不发生 |
sin21°+sin22°+sin23°+sin288°+sin289°+sin290°=( )
| A、45 | ||||
B、45
| ||||
C、
| ||||
D、
|