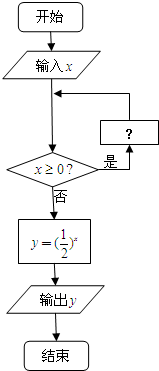
题目内容
7.设I为△ABC内心,BC=a,AC=b,AB=c,I在BC、AC、AB边上的射影分别为D、E、F,内切圆半径为r,含p=$\frac{1}{2}$(a+b+c)求证:abc•r=p•AI•BI•CI.
分析 通过正弦定理可知$\frac{AI}{c}$=$\frac{sin\frac{B}{2}}{cos\frac{C}{2}}$、$\frac{BI}{a}$=$\frac{sin\frac{C}{2}}{cos\frac{A}{2}}$、$\frac{CI}{b}$=$\frac{sin\frac{A}{2}}{cos\frac{B}{2}}$,计算可知$\frac{AI•BI•CI}{abc}$=$\frac{r}{p-a}$•$\frac{r}{p-b}$•$\frac{r}{p-c}$,通过三角形面积公式可知(p-a)(p-b)(p-c)=pr2,进而化简即得结论.
解答 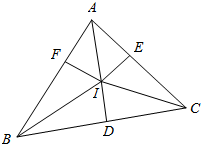 证明:如图,由正弦定理可知$\frac{AI}{c}$=$\frac{sin\frac{B}{2}}{sin∠AIB}$=$\frac{sin\frac{B}{2}}{sin(90°+\frac{C}{2})}$=$\frac{sin\frac{B}{2}}{cos\frac{C}{2}}$,
证明:如图,由正弦定理可知$\frac{AI}{c}$=$\frac{sin\frac{B}{2}}{sin∠AIB}$=$\frac{sin\frac{B}{2}}{sin(90°+\frac{C}{2})}$=$\frac{sin\frac{B}{2}}{cos\frac{C}{2}}$,
同理可知$\frac{BI}{a}$=$\frac{sin\frac{C}{2}}{cos\frac{A}{2}}$,$\frac{CI}{b}$=$\frac{sin\frac{A}{2}}{cos\frac{B}{2}}$,
∴$\frac{AI•BI•CI}{abc}$=tan$\frac{A}{2}$tan$\frac{B}{2}$tan$\frac{C}{2}$
=$\frac{r}{AF}$•$\frac{r}{BD}$•$\frac{r}{CE}$
=$\frac{2r}{b+c-a}$•$\frac{2r}{c+a-b}$•$\frac{2r}{a+b-c}$
=$\frac{r}{p-a}$•$\frac{r}{p-b}$•$\frac{r}{p-c}$,
又∵p(p-a)(p-b)(p-c)=${{S}_{△ABC}}^{2}$=p2r2,
∴$\frac{AI•BI•CI}{abc}$=$\frac{{r}^{3}}{p{r}^{2}}$=$\frac{r}{p}$,
整理得:abc•r=p•AI•BI•CI.
点评 本题考查解三角形,考查运算求解能力,利用正弦定理及三角形面积公式是解决本题的关键,注意解题方法的积累,属于难题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
| A. | 工序流程图 | B. | 知识结构图 | C. | 程序框图 | D. | 组织结构图 |