题目内容
2.若数列{an}(n∈N*)是等差数列,则有数列${b_n}=\frac{{{a_1}+{a_2}+…+{a_n}}}{n}$(n∈N*) 也是等差数列;类比上述性质,相应地:若数列{cn}是等比数列,且cn>0,则有数列dn=$\root{n}{{{c_1}{c_2}{c_3}…{c_n}}}$ (n∈N*)也是等比数列.分析 在类比等差数列的性质推理等比数列的性质时,由加法类比推理为乘法,由减法类比推理为除法,由算术平均数类比推理为几何平均数等,可得结论.
解答 解:数列{an},(n∈N*)是等差数列,则有数列${b_n}=\frac{{{a_1}+{a_2}+…+{a_n}}}{n}$(n∈N*)也是等差数列.
类比推断:若数列{cn}是各项均为正数的等比数列,则当dn=$\root{n}{{{c_1}{c_2}{c_3}…{c_n}}}$时,数列{dn}也是等比数列.
故答案为:$\root{n}{{{c_1}{c_2}{c_3}…{c_n}}}$.
点评 本题主要考查了类比推理,找出两类事物之间的相似性或一致性,用一类事物的性质去推测另一类事物的性质,得出一个明确的命题,属于中档题.

练习册系列答案
相关题目
17.通过圆与球的类比,由“半径为R的圆的内接矩形中,以正方形的面积为最大,最大值为2R2”,猜想关于球的相应命题为( )
| A. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为2R3 | |
| B. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为3R3 | |
| C. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为$\frac{4\sqrt{3}}{9}$R3 | |
| D. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为$\frac{8\sqrt{3}}{9}$R3 |
11.上面程序框图的结构中最突出的逻辑结构及输出的i的值是( )
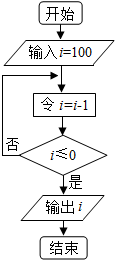

| A. | 当型循环结构,-1 | B. | 当型循环结构,0 | ||
| C. | 直到型循环结构,0 | D. | 直到型循环结构,-1 |
12.执行如图所示的程序框图,则输出的S值为( )


| A. | 4 | B. | 6 | C. | 8 | D. | 16 |