题目内容
16.函数f1(x)=x,f2(x)=x-$\frac{{x}^{3}}{6}$,f3(x)=x-$\frac{{x}^{3}}{6}$+$\frac{{x}^{5}}{120}$,f4(x)=x-$\frac{{x}^{3}}{6}$+$\frac{{x}^{5}}{120}$-$\frac{{x}^{7}}{5040}$,f5(x)=x-$\frac{{x}^{3}}{6}$+$\frac{{x}^{5}}{120}$-$\frac{{x}^{7}}{5040}$+$\frac{{x}^{9}}{362880}$,依次称为f(x)=sinx在[0,π]上的第1项、2项、3项、4项、5项多项式逼近函数.以此类推,请将f(x)=sinx的n项多项式逼近函数fn(x)在横线上补充完整:fn(x)=$x-\frac{x^3}{3!}+\frac{x^5}{5!}-…+{(-1)^{n-1}}\frac{{{x^{2n-1}}}}{(2n-1)!}$.分析 由函数f(x)=sinx的第1项、2项、3项、4项、5项多项式逼近函数,分析各项中符号,分子,分母的变化规律,归纳推理后可得f(x)=sinx的n项多项式逼近函数fn(x)的解析式
解答 解:由函数f1(x)=x,f2(x)=x-$\frac{{x}^{3}}{6}$,f3(x)=x-$\frac{{x}^{3}}{6}$+$\frac{{x}^{5}}{120}$,f4(x)=x-$\frac{{x}^{3}}{6}$+$\frac{{x}^{5}}{120}$-$\frac{{x}^{7}}{5040}$,f5(x)=x-$\frac{{x}^{3}}{6}$+$\frac{{x}^{5}}{120}$-$\frac{{x}^{7}}{5040}$+$\frac{{x}^{9}}{362880}$,可得函数的解析式中共有2n-1项,其中各项符号由(-1)n-1确定;分子为x2n-1,分母为(2n-1)!,
∴fn(x)=$x-\frac{x^3}{3!}+\frac{x^5}{5!}-…+{(-1)^{n-1}}\frac{{{x^{2n-1}}}}{(2n-1)!}$.
故答案为:$x-\frac{x^3}{3!}+\frac{x^5}{5!}-…+{(-1)^{n-1}}\frac{{{x^{2n-1}}}}{(2n-1)!}$.
点评 本题考查的知识点是归纳推理,其中根据函数f(x)=sinx的第1项、2项、3项、4项、5项多项式逼近函数,分析各项中符号,分子,分母的变化规律是解答的关键.

练习册系列答案
相关题目
11.上面程序框图的结构中最突出的逻辑结构及输出的i的值是( )
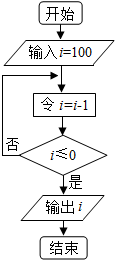

| A. | 当型循环结构,-1 | B. | 当型循环结构,0 | ||
| C. | 直到型循环结构,0 | D. | 直到型循环结构,-1 |
8.如图,若依次输入的x分别为$\frac{5π}{6}$、$\frac{π}{6}$,相应输出的y分别为y1、y2,则y1、y2的大小关系是( )
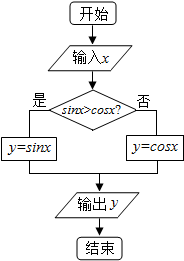

| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
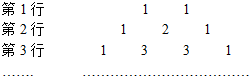 如图,在杨辉三角中,若某行存在相邻的三个数成等差数列,则称此行为“A-P行”.从上往下数,第1个A-P行的行序号是7,第k个A-P行的行序号是(k+2)2-2.
如图,在杨辉三角中,若某行存在相邻的三个数成等差数列,则称此行为“A-P行”.从上往下数,第1个A-P行的行序号是7,第k个A-P行的行序号是(k+2)2-2.