题目内容
16.已知点P在圆x2+y2=1上,点A的坐标为(-2,0),O为原点,则$\overrightarrow{AO}$•$\overrightarrow{AP}$的最大值为6.分析 设P(cosα,sinα).可得$\overrightarrow{AO}$=(2,0),$\overrightarrow{AP}$=(cosα+2,sinα).利用数量积运算性质、三角函数的单调性与值域即可得出.
解答 解:设P(cosα,sinα).$\overrightarrow{AO}$=(2,0),$\overrightarrow{AP}$=(cosα+2,sinα).
则$\overrightarrow{AO}$•$\overrightarrow{AP}$=2(cosα+2)≤6,当且仅当cosα=1时取等号.
故答案为:6.
点评 本题考查了数量积运算性质、三角函数的单调性与值域、圆的参数方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
4.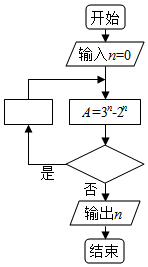 如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在
如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在 和
和 两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )
 如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在
如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在 和
和 两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )| A. | A>1000和n=n+1 | B. | A>1000和n=n+2 | C. | A≤1000和n=n+1 | D. | A≤1000和n=n+2 |
8.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
5.若双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线被圆(x-2)2+y2=4所截得的弦长为2,则C的离心率为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
10.已知集合P={x|-1<x<1},Q={x|0<x<2},那么P∪Q=( )
| A. | (-1,2) | B. | (0,1) | C. | (-1,0) | D. | (1,2) |
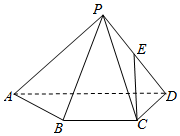 如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.