题目内容
若函数y=mx2-4x+1的图象与x轴有公共点,则m的范围是 .
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:函数y=mx2-4x+1的图象与x轴有公共点可化为方程mx2-4x+1=0有解;讨论方程的次数.
解答:
解:函数y=mx2-4x+1的图象与x轴有公共点可化为
方程mx2-4x+1=0有解.
①若m=0,成立,
②若m≠0,则△=16-4m≥0,
则m≤4,
故答案为:m≤4.
方程mx2-4x+1=0有解.
①若m=0,成立,
②若m≠0,则△=16-4m≥0,
则m≤4,
故答案为:m≤4.
点评:本题考查了函数的零点与方程的根的关系及方程的次数讨论,属于基础题.

练习册系列答案
相关题目
已知不等式-2xy≤ax2+2y2,若对任意x∈[1,2]及y∈[-1,3]不等式恒成立,则实数a的范围是( )
A、0≤a≤
| ||
| B、a≥0 | ||
C、a≥
| ||
D、a≥-
|
定义在R上的偶函数f(x),满足f(x+2)=f(x),且在区间[-1,0]上为递增,则( )
A、f(
| ||
B、f(2)<f(3)<f(
| ||
C、f(3)<f(2)<f(
| ||
D、f(3)<f(
|
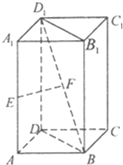 如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.
如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.