题目内容
 如图,在正三棱锥S-ABC中,M、N分别是侧棱SB、SC的中点,若截面AMN⊥侧面SBC,则此三棱锥的侧棱与底面所成角的正切值是( )
如图,在正三棱锥S-ABC中,M、N分别是侧棱SB、SC的中点,若截面AMN⊥侧面SBC,则此三棱锥的侧棱与底面所成角的正切值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:棱锥的结构特征
专题:计算题,空间位置关系与距离,空间角
分析:利用截面AMN⊥侧面PBC的特点,证明△PAD是等腰三角形,从而沟通了侧棱长和底面高间的关系,过S作SH⊥底面ABC,垂足为H,则三棱锥的侧棱与底面所成角为∠SAH,最后在直角三角形中计算tan∠SAH即可.
解答:
解:如图,取MN中点O,连接AO,SO,延长SO交BC于点D,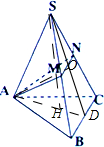
连接AD,则BD=DC,
∵三棱锥S-ABC为正三棱锥,∴AM=AN∴AO⊥MN
∵截面AMN⊥侧面SBC,
∴AO⊥侧面SBC,
∴AO⊥SD,又SO=OD,∴SA=AD,
过S作SH⊥底面ABC,垂足为H,H为底面的中心,AH=
AD,
则三棱锥的侧棱与底面所成角为∠SAH,
在直角三角形SAH中,SH=
=
AD,
故tan∠SAH=
=
.
故选:A.

连接AD,则BD=DC,
∵三棱锥S-ABC为正三棱锥,∴AM=AN∴AO⊥MN
∵截面AMN⊥侧面SBC,
∴AO⊥侧面SBC,
∴AO⊥SD,又SO=OD,∴SA=AD,
过S作SH⊥底面ABC,垂足为H,H为底面的中心,AH=
| 2 |
| 3 |
则三棱锥的侧棱与底面所成角为∠SAH,
在直角三角形SAH中,SH=
| SA2-AH2 |
| ||
| 3 |
故tan∠SAH=
| SH |
| AH |
| ||
| 2 |
故选:A.
点评:本题考查了正三棱锥的性质,线面角的求法和面面垂直的性质,解题时要有空间想象力,要能恰当的沟通未知量之间的关系,能够用转化的思想方法将空间问题化为平面问题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
在区间(110,120]内的所有实数中,随机抽取一个实数a,则这个实数a<113的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数g(x)=2013x,a、b∈R+,A=g(
),B=g(
),C=g(
),则A、B、C的大小关系为( )
| a+b |
| 2 |
| ab |
| 2ab |
| a+b |
| A、C≤B≤A |
| B、A≤C≤B |
| C、B≤C≤A |
| D、A≤B≤C |
 如图,在正方形ABCD中,E是AB中点,F是AD上一点,且AF=
如图,在正方形ABCD中,E是AB中点,F是AD上一点,且AF=| 1 |
| 4 |
| A、EF•EC=EG•FC |
| B、EC2=CG•GF |
| C、AE2+AF2=FG•FC |
| D、EG2=GF•GC |
已知f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,对任意的x∈[t,t+2]不等式f(x+t)≥2f(x)恒成立,那么实数t的取值范围是( )
A、[
| ||
| B、[2,+∞) | ||
C、(0,
| ||
D、[0,
|
已知集合A={x|x2-2x-3<0},B={x||x|<2},则A∩B等于( )
| A、{x|-1<x<2} |
| B、{x|2<x<3} |
| C、{x|x<-1} |
| D、{x|x>3} |
设函数y1=ln(1-x)定义域为A,函数y2=ex-1的值域为B,则A∩B是( )
| A、∅ | B、R |
| C、(0,1) | D、(-1,1) |
 设函数y=f(x)的导函数为f′(x).若f′(x)的图象如图所示,则函数y=f(x)的图象可能是( )
设函数y=f(x)的导函数为f′(x).若f′(x)的图象如图所示,则函数y=f(x)的图象可能是( )


