题目内容
下列函数中,既是偶函数又在区间(-∞,0)上单调递增的是( )
| A、f(x)=2-x | ||
| B、f(x)=x2+1 | ||
C、f(x)=
| ||
| D、f(x)=x3 |
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:首先从函数的奇偶性排除部分选项,然后再判断函数的单调性
解答:
解:在四个选项中,选项A,f(-x)=2x,f(-x)≠f(x);f(-x)≠-f(x),所以是非奇非偶的函数;
选项B,f(-x)=(-x)2+1=x2+1=f(x),是偶函数,但是在区间(-∞,0)上单调递减;
选项C,f(-x)=
=
=f(x),是偶函数,在区间(-∞,0)上单调递增;
选项D,f(-x)=(-x)3=-x3=-f(x),是奇函数;
综上既是偶函数又在区间(-∞,0)上单调递增的是C;
故选C.
选项B,f(-x)=(-x)2+1=x2+1=f(x),是偶函数,但是在区间(-∞,0)上单调递减;
选项C,f(-x)=
| 1 |
| (-x)2 |
| 1 |
| x2 |
选项D,f(-x)=(-x)3=-x3=-f(x),是奇函数;
综上既是偶函数又在区间(-∞,0)上单调递增的是C;
故选C.
点评:本题考查了函数的奇偶性的判断和单调性的判断,一般从定义入手,经常考查,属于基础题.

练习册系列答案
相关题目
若集合A={x|log2x<2},B={x|lg(x-1)≤1},则A∩B=( )
| A、{x|0<X≤11} |
| B、{x|1<X<4} |
| C、{x|0<X<4} |
| D、{x|0<X<11} |
下列函数中,在R上单调递增的是( )
| A、y=|x| | ||
| B、y=lnx | ||
C、y=(
| ||
| D、y=x3 |
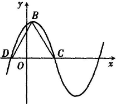 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图,B为图象的最高点,C、D为图象与x轴的交点,△BCD为正三角形,且S△BCD=4
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图,B为图象的最高点,C、D为图象与x轴的交点,△BCD为正三角形,且S△BCD=4