题目内容
19.98和63的最大公约数为7.分析 本题考查的知识点是辗转相除法,根据辗转相除法的步骤,将98和63代入易得到答案.
解答 解:98=63×1+35,
63=35×1+28,
35=28×1+7,
28=7×4,
故98和63的最大公约数为7,
故答案为:7
点评 对任意整数a,b,b>0,存在唯一的整数q,r,使a=bq+r,其中0≤r<b,这个事实称为带余除法定理,若c|a,c|b,则称c是a,b的公因数.若d是a,b的公因数,且d可被a,b的任意公因数整除则称d是a,b的最大公因数.当d≥0时,d是a,b公因数中最大者.若a,b的最大公因数等于1,则称a,b互素.累次利用带余除法可以求出a,b的最大公因数,这种方法常称为辗转相除法.

练习册系列答案
相关题目
4.从{-3,-2,-1,0,1,2,3}中,任取3个不同的数作为抛物线的方程y=ax2+bx+c(a≠0)的系数,使抛物线过原点,且顶点在第一象限这样的抛物线共有( )条.
| A. | 9 | B. | 6 | C. | 12 | D. | 7 |
14.已知关于某设各的使用年限x(单位:年)和所支出的维修费用y(单位:万元)有如下的统计资料,
由上表可得线性回归方程$\widehaty=\widehatbx+0.08$,若规定当维修费用y>12时该设各必须报废,据此模型预报该设各使用年限的最大值为( )
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
9.设x,y∈R,则“x>y>0”是“$\frac{x}{y}$>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
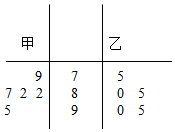 甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下:
甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下: