题目内容
平面向量
,
,
满足|
|=1,
•
=1,
•
=2,|
-
|=2,则
•
的最小值为 .
| a |
| b |
| e |
| e |
| a |
| e |
| b |
| e |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,建立直角坐标系.由|
|=1,不妨设
=(1,0).由
•
=1,
•
=2,可设
=(1,m),
=(2,n).利用|
-
|=2,可得
=2,(m+n)2=3+4mn≥0,再利用数量积运算
•
=2+mn即可得出.
| e |
| e |
| a |
| e |
| b |
| e |
| a |
| b |
| a |
| b |
| 1+(m-n)2 |
| a |
| b |
解答:
解:如图所示,建立直角坐标系.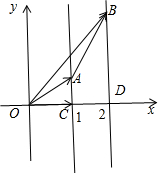
∵|
|=1,∴不妨设
=(1,0).
∵
•
=1,
•
=2,
∴可设
=(1,m),
=(2,n).
∴
-
=(-1,m-n).
∵|
-
|=2,
∴
=2,化为(m-n)2=3,
∴(m+n)2=3+4mn≥0,
∴mn≥-
,当且仅当m=-n=±
时取等号.
∴
•
=2+mn≥2-
=
.
故答案为:
.

∵|
| e |
| e |
∵
| a |
| e |
| b |
| e |
∴可设
| a |
| b |
∴
| a |
| b |
∵|
| a |
| b |
∴
| 1+(m-n)2 |
∴(m+n)2=3+4mn≥0,
∴mn≥-
| 3 |
| 4 |
| ||
| 2 |
∴
| a |
| b |
| 3 |
| 4 |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查了通过建立直角坐标系解决向量有关问题、数量积运算及其性质、不等式的性质,考查了推理能力和解决问题的能力,属于难题.

练习册系列答案
相关题目
 一个侧棱与底面垂直的棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则截去那一部分的体积为.( )
一个侧棱与底面垂直的棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则截去那一部分的体积为.( )| A、1 | ||
B、
| ||
| C、11 | ||
| D、12 |
 已知某几何体的三视图如图,其中主视图中半圆直径为2,则该几何体的体积
已知某几何体的三视图如图,其中主视图中半圆直径为2,则该几何体的体积