已知集合A={-1.0.1}.B={y|y=x2.x∈A}.则A∩B=( )A．{0.1}B．{-1.1}C．{-1.0}D．{-1.0.1} 题目和参考答案——青夏教育精英家教网——

题目内容

12．已知集合A={-1，0，1}，B={y|y=x²，x∈A}，则A∩B=（　　）

A．

{0，1}

B．

{-1，1}

C．

{-1，0}

D．

{-1，0，1}

分析由二次函数的值域求法，运用列举法化简集合B，再由交集的定义，即可得到所求．

解答解：集合A={-1，0，1}，
B={y|y=x²，x∈A}={0，1}，
则A∩B={0，1}，
故选：A．

点评本题考查集合的运算，主要是交集的求法，注意运用列举法和二次函数的值域，以及集合中元素的互异性，属于基础题．

练习册系列答案

口算题卡延边大学出版社系列答案

英才教程奇迹课堂口算题卡系列答案

A加金题系列答案

学习方案系列答案

全优测试卷系列答案

新课标学案高考调研系列答案

凤凰新学案系列答案

名师特攻百分好题测评卷系列答案

单元加期末100分冲刺卷系列答案

单元月考期末测评卷系列答案

相关题目

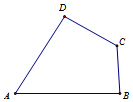如图，A，B，C，D为平面四边形ABCD的四个内角，若A+C=180°，AB=6，BC=4，CD=5，AD=5，则四边形ABCD面积是10$\sqrt{6}$．

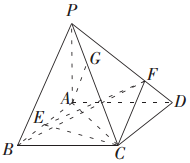已知四棱锥P-ABCD的底面ABCD是平行四边形，△PAB与△ABC是等腰三角形，PA⊥平面ABCD，PA=2，AD=2$\sqrt{2}$，AC⊥BA，点E是线段AB上靠近点B的一个三等分点，点F、G分别在线段PD，PC上．
（Ⅰ）证明：CD⊥AG；
（Ⅱ）若三棱锥E-BCF的体积为$\frac{1}{6}$，求$\frac{FD}{PD}$的值．

20．若正方形ABCD的边长为$2，\overrightarrow{BC}=2\overrightarrow{BE}，\overrightarrow{DC}=λ\overrightarrow{DF}$，若$\overrightarrow{AE}•\overrightarrow{AF}=1$，则λ的值为-4．

7．若函数$f（x）=sin2ωx+2\sqrt{3}{cos^2}ωx-\sqrt{3}（ω＞0）$在$[\frac{π}{2}，π]$上单调递减，则ω的取值范围是（　　）

$[\frac{1}{6}，\frac{1}{4}]$

$[\frac{1}{6}，\frac{7}{12}]$

$[\frac{1}{4}，\frac{1}{2}]$

$[0，\frac{1}{2}]$

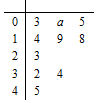已知函数f（x）=x²+$\sqrt{2}（m-1）x+\frac{m}{4}$，现有一组数据，绘制得到茎叶图，且茎叶图中的数据的平均数为2．（茎叶图中的数据均为小数，其中茎为整数部分，叶为小数部分）
（Ⅰ）求a的值；
（Ⅱ）现从茎叶图小于3的数据中任取2个数据分别替换m的值，求恰有1个数据使得函数f（x）没有零点的概率．

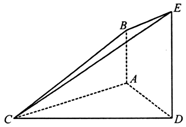如图，已知AB⊥平面ACD，DE∥AB，△ACD是等腰三角形，∠CAD=120°，AD=DE=2AB．
（I）求证：平面BCE⊥平面CDE；
（II）求平面BCE与平面ADEB所成锐二面角的余弦值．

1．已知函数f（x）=（x+5）（x²+x+a）的图象关于点（-2，0）对称，设关于x的不等式f′（x+b）＜f′（x）的解集为M，若（1，2）⊆M，则实数b的取值范围是[-6，0）．

2．不等式组$\left\{\begin{array}{l}{x≥2}\\{x+y≥6}\\{x-2y≤0}\end{array}\right.$，所表示的平面区域为T，若直线mx-y+m+1=0与T有公共点，实数m的取值范围是（　　）

（$\frac{1}{5}$，+∞）

[$\frac{1}{5}$，+∞）