题目内容
8.已知P(x,y)为区域$\left\{\begin{array}{l}{{y}^{2}-4{x}^{2}≤0}\\{0≤x≤a}\end{array}\right.$内的任意一点,当该区域的面积为2时,z=x+2y的最大值是5.分析 作出不等式组对应的平面区域.根据三角形的面积求出a的值,利用数形结合进行求解即可.
解答 解:不等式组等价为$\left\{\begin{array}{l}{(y-2x)(y+2x)≤0}\\{0≤x≤a}\end{array}\right.$,
即$\left\{\begin{array}{l}{y-2x≥0}\\{y+2x≤0}\\{0≤x≤a}\end{array}\right.$ 或$\left\{\begin{array}{l}{y-2x≤0}\\{y+2x≥0}\\{0≤x≤a}\end{array}\right.$,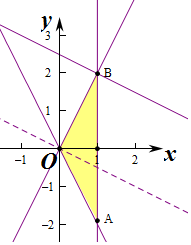
则A(a,-2a),B(a,2a),
由S△OAB=$\frac{1}{2}$•4a•a=2,得a=1.
∴B(1,2),
由z=x+2y得y=$-\frac{1}{2}$x+$\frac{z}{2}$,
∴当y=$-\frac{1}{2}$x+$\frac{z}{2}$过B点时,z最大,z=1+2×2=5.
故答案为:5
点评 本题主要考查线性规划的基本应用,利用z的几何意义是解决线性规划问题的关键,注意利用数形结合来解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知x和y是实数,i是虚数单位,(1+i)x+yi=(1+3i)i,则|x+yi|等于( )
| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{11}$ | D. | $\sqrt{17}$ |
13.已知θ∈(π,2π),$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(cosθ,sinθ),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则cosθ的值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | ±$\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
2.下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的是( )
| A. | $y=\frac{1}{x}$ | B. | y=2|x| | C. | $y=ln\frac{1}{|x|}$ | D. | y=x3 |