Question

如图所示，C，D是两个小区的所在地，C，D到一条公路AB的垂直距离分别为CA=1km，DB=2km，AB两地之间的距离为4km
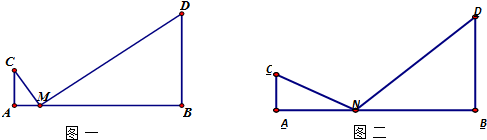
（1）如图一所示，某移动公司将在AB之间找一点M，在M处建造一个信号塔，使得M对C，D的张角与M对C，A的张角相等，试确定点M到点A的距离；
（2）如图二所示，某公交公司将在AB之间找一点N，在N处建造一个公交站台，使得N对C，D两个小区的视角∠CND最大，试确定点N到点A的距离．

Answer 1

考点：二倍角的正切,两角和与差的正切函数

专题：应用题,解三角形

分析：（1）设MA=x，∠CMA=α，则∠CMD=α，∠BMD=π-2α．依题意，可用x表示出tanα，tan2α，由二倍角的正切可解得x的值，即求出点M到点A的距离；
（2）设∠CNA=α，∠DNB=β，则∠CND=π-（α+β），设NB=4-x，所以tanα，tanβ，tan∠CND=

x+4

x2-4x+2

，即可求出最大的角∠CND，确定点N到点A的距离．

解答： 解：（1）设MA=x，∠CMA=α，
则∠CMD=α，∠BMD=π-2α．
依题意，tanα=

1

x

，tan2α=-

2

4-x

，
由tan2α=

2tanα

1-tan2a

得

-2

4-x

=

2 x

1- 1 x

，解得x=

1

4

，
故点M到点A的距离为

1

4

km．
（2）设∠CNA=α，∠DNB=β，则∠CND=π-（α+β）．
设NB=4-x，所以tanα=

1

x

，tanβ=

2

4-x

，tan∠CND=tan[π-(α+β)]=-tan(α+β)=

x+4

x2-4x+2

，
记f(x)=

x+4

x2-4x+2

，(0＜x＜4)，f（x）=

x+4

x2-4x+2

，（0＜x＜4，且x≠2±

2

），
对x的范围进行分类讨论：
①当x接近这2±

2

这两个值时，f（x）趋近于正无穷，此时∠CDN为90°；
②当x≠2±

2

时，0＜x＜2-

2

或2+

2

＜x＜4时，∠CDN为锐角；
③当 2-

2

＜x＜2+

2

时，∠CDN为钝角；
令x+4=t，则6-

2

＜t＜6+

2

，
有f(x)=

t

t2-12t+34

=

1

t+ 34 t -12

≤

1

2 34 -12

=-

6+ 34

4

，
故当且仅当t=

34

时，ymax=-

6+ 34

4

，此时∠CDN最大，对应地，x=t-4=-4+

34

．

点评：本题主要考察了两角和与差的正切函数公式的应用，解三角形的实际应用，考查了利用基本不等式求最值，解答的关键是把实际问题转化为数学问题，是中档题．