题目内容
已知集合A={x|x2-2x-3≥0}，B={x|-2≤x＜2}，则A∩B=（ ）
| A、[1，2） |
| B、[-1，1] |
| C、[-1，2） |
| D、[-2，-1] |
考点：交集及其运算
专题：集合
分析：求出A中不等式的解集确定出A，找出A与B的交集即可．
解答：
解：由A中不等式变形得：（x-3）（x+1）≥0，
解得：x≥3或x≤-1，即A=（-∞，-1]∪[3，+∞），
∵B=[-2，2），
∴A∩B=[-2，-1]．
故选：D．
解得：x≥3或x≤-1，即A=（-∞，-1]∪[3，+∞），
∵B=[-2，2），
∴A∩B=[-2，-1]．
故选：D．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
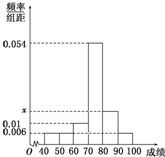某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：