题目内容
1.函数y=$\frac{ln|x|}{{x}^{2}}+\frac{1}{{x}^{2}}$在[-2,2]的图象大致为( )| A. | 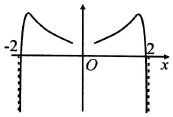 | B. |  | ||
| C. | 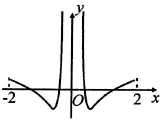 | D. |  |
分析 根据当x=2时,y=$\frac{1+ln2}{4}$>0,故排除A、D.当x>0时,利用导数求得函数在(0,$\sqrt{e}$)上单调递增,在($\sqrt{e}$,+∞)上单调递减,从而得出结论.
解答 解:对于函数y=$\frac{lnx+1}{{x}^{2}}$,故当x=2时,y=$\frac{1+ln2}{4}$>0,故排除A、D;
当x>0时,由于y′=$\frac{\frac{1}{x}{•x}^{2}-2xlnx}{{x}^{4}}$=$\frac{1-2lnx}{{x}^{3}}$,令y′=0,求得x=$\sqrt{e}$,
在(0,$\sqrt{e}$)上,y′>0,函数y单调递增;在($\sqrt{e}$,+∞)上,y′<0,函数y单调递减,
故排除C,
故选:B.
点评 本题主要考查函数的图象,利用导数研究函数的单调性,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
12.在等比数列{an}中,a1,a4是方程x2-2x-3=0的两根,则a2•a3=( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
9.设f(x)=$\left\{{\begin{array}{l}{-2{e^{x-2}},x≥2}\\{{{log}_3}({{x^2}-1}),x<2}\end{array}}$,则f(f(2))的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
16.在矩形中ABCD中,AB=2AD,在CD上任取一点P,△ABP的最大边是AB的概率是( )
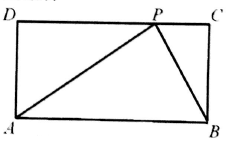

| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-1$ |
6.已知等比数列{an}中,各项都是正数,且${a_1},\frac{1}{2}{a_3},2{a_2}$成等差数列,则$\frac{{{a_8}+{a_9}}}{{{a_7}+{a_8}}}$=( )
| A. | $\sqrt{2}-1$ | B. | $3-2\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $\sqrt{2}+1$ |
10.从4,5,6,7,8这5个数中任取两个数,则所取两个数之积能被3整除概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |