题目内容
5.若tanθ=$\frac{1}{2}$,则cos2θ=$\frac{3}{5}$.分析 利用二倍角的余弦函数公式,同角三角函数基本关系式化简所求即可计算得解.
解答 解:∵tanθ=$\frac{1}{2}$,
∴cos2θ=$\frac{co{s}^{2}θ-si{n}^{2}θ}{co{s}^{2}θ+si{n}^{2}θ}$=$\frac{1-ta{n}^{2}θ}{1+ta{n}^{2}θ}$=$\frac{1-\frac{1}{4}}{1+\frac{1}{4}}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题主要考查了二倍角的余弦函数公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
16.在矩形中ABCD中,AB=2AD,在CD上任取一点P,△ABP的最大边是AB的概率是( )
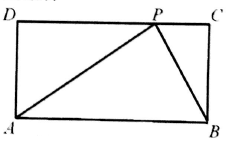

| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-1$ |
10.从4,5,6,7,8这5个数中任取两个数,则所取两个数之积能被3整除概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
15.曲线f(x)=x3+x-2在点P处的切线平行于直线4x-y-1=0,则点P的坐标为( )
| A. | (1,0) | B. | (2,8) | C. | (1,0)或(-1,-4) | D. | (2,8)或(-1,-4) |