题目内容
4．
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各面中，最长棱的长度是（ ）| A． | $2\sqrt{5}$ | B． | $4\sqrt{2}$ | C． | 6 | D． | $4\sqrt{3}$ |
分析 根据三视图得出该几何体是在棱长为4的正方体中的三棱锥，画出图形，得出最长的棱长是哪一条，求出值即可．
解答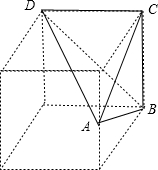 
解：根据题意，得几何体如图；
该几何体是三棱锥A-BCD，
且该三棱锥是放在棱长为4的正方体中，
所以，在三棱锥A-BCD中，最长的棱长为AD，
且AD=$\sqrt{C{D}^{2}+A{C}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}+{2}^{2}}=\sqrt{36}$=6．
故选C．
点评 本题考查了空间几何体三视图的应用问题，解题的关键是由三视图还原为几何体．
练习册系列答案
教材全解字词句篇系列答案
相关题目
14．
如图所示的程序框图的算符源于我国古代的“中国剩余定理”，用N≡n（modm）表示正整数N除以正整数m后的余数为n，例如：7≡1（mod3），执行该程序框图，则输出的n的值为（ ）
如图所示的程序框图的算符源于我国古代的“中国剩余定理”，用N≡n（modm）表示正整数N除以正整数m后的余数为n，例如：7≡1（mod3），执行该程序框图，则输出的n的值为（ ）| A． | 19 | B． | 20 | C． | 21 | D． | 22 |
15．已知函数f（x）=$\left\{\begin{array}{l}\frac{{{2^x}+2}}{2}，x≤1\\|ln（{x-1}）|，x＞1\end{array}$，则函数F（x）=f[f（x）]-af（x）-$\frac{3}{2}$的零点个数是4个时，下列选项是a的取值范围的子集的是（ ）
| A． | $（{\frac{1}{2}，+∞}）∪\left\{{\frac{ln2}{2}}\right\}$ | B． | $[{\frac{ln2}{2}，+∞}）$ | C． | $（{0，\frac{1}{2}}）∪\left\{{\frac{ln2}{2}}\right\}$ | D． | $[{\frac{ln2}{2}，\frac{1}{2}}）$ |
8．已知集合A={x|$\frac{x-1}{x+2}$≤0}，B={x|x＜-2}，则A∪（∁UB）=（ ）
| A． | [-2，+∞） | B． | （-2，+∞） | C． | [-2，1] | D． | （-2，1] |