已知全集U={0.1.2.3.4}.集合A={1.2.3}.B={2.4}.则(∁UB)∪A为( )A．{1.3}B．{2.3.4}C．{0.1.2.3}D．{0.2.3.4} 题目和参考答案——青夏教育精英家教网——

题目内容

3．已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，则（∁_UB）∪A为（　　）

A．

{1，3}

B．

{2，3，4}

C．

{0，1，2，3}

D．

{0，2，3，4}

分析根据补集与并集的定义，计算即可．

解答解：全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，
则∁_UB={0，1，3}，
∴（∁_UB）∪A={0，1，2，3}．
故选：C．

点评本题考查了集合的定义与运算问题，是基础题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

13．从含有4件正品、2件次品的6件产品中，随机抽取3件，则恰好抽到1件次品的概率（　　）

14．已知$\frac{4+mi}{1+2i}$∈R，且m∈R，则|m+6i|=（　　）

若输入5，如图中所示程序框图运行后，输出的结果是（　　）

18．如图，已知$\overrightarrow{CA}=\overrightarrow a$，$\overrightarrow{CB}=\overrightarrow b$，AD=2DB，用$\overrightarrow a$、$\overrightarrow b$表示$\overrightarrow{DC}$为（　　）

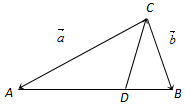
$\overrightarrow{DC}=-\frac{5}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$

$\overrightarrow{DC}$=$-\frac{1}{2}\overrightarrow a-\frac{1}{3}\overrightarrow b$

$\overrightarrow{DC}$=$-\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$

$\overrightarrow{DC}=-\frac{1}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$

已知函数f（x）=|x+1|-|2x-3|．
（Ⅰ）在图中画出y=f（x）的图象；
（Ⅱ）求不等式|f（x）|＞1的解集．

15．已知f（x）=2xlnx，g（x）=x³+ax²-x+2．
（1）如果函数g（x）的单调递减区间为$（-\frac{1}{3}，1）$，求函数g（x）的解析式；
（2）在（1）的条件下，求函数y=g（x）的图象在点P（-1，g（-1））处的切线方程；
（3）已知不等式f（x）≤g'（x）+2恒成立，若方程ae^a-m=0恰有两个不等实根，求m的取值范围．

12．数列a_n=2ⁿ⁺¹，其前n项和为T_n，若不等式nlog₂（T_n+4）-λ（n+1）+7≥3n对一切n∈N^*恒成立，则实数λ的取值范围为（　　）

13．函数y=x³-ax在x=1处有极值，则实数a为3．