题目内容
19.已知数列{an}的通项公式为an=$\frac{3}{2n-7}$,记数列{an}的前n项和为Sn,则使Sn≤0成立的n的最大值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
分析 an=$\frac{3}{2n-7}$,数列{an}的前n项和为Sn=$-\frac{3}{5}$-1-3+…+$\frac{3}{2n-7}$,由于Sn+1-Sn=$\frac{3}{2n-5}$,可得:n≤2时,Sn+1<Sn;n≥3时,Sn+1>Sn.经过计算即可得出.
解答 解:∵an=$\frac{3}{2n-7}$,
∴数列{an}的前n项和为Sn=$-\frac{3}{5}$-1-3+…+$\frac{3}{2n-7}$,
可得:Sn+1-Sn=$\frac{3}{2n-5}$,
n≤2时,Sn+1<Sn;n≥3时,Sn+1>Sn.
∴S1>S2>S3<S4<S5<S6<…,
S1=$-\frac{3}{5}$<0,S2<0,S3=-$\frac{23}{5}$<0,S4=-$\frac{8}{5}$<0,S5=$-\frac{3}{5}$<0,S6=0,n≥7时,Sn>0.
则使Sn≤0成立的n的最大值为6.
故选:C.
点评 本题考查了递推关系、数列的单调性、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.已知函数g(x)=x-1,函数f(x)满足f(x+1)=-2f(x)-1,当x∈(0,1]时,f(x)=x2-x,对于?x1∈(1,2],?x2∈R,则(x1-x2)2+(f(x1)-g(x2))2的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{49}{128}$ | C. | $\frac{81}{128}$ | D. | $\frac{125}{128}$ |
14.如图所示的程序框图,若输入n的值为5,则输出s的值为( )


| A. | 7 | B. | 8 | C. | 10 | D. | 11 |
4. 菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,使用时需要用清水清洗干净,如表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的统计表:
菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,使用时需要用清水清洗干净,如表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的统计表:
(Ⅰ)在如图的坐标系中,描出散点图,并判断变量x与y的相关性;
(Ⅱ)若用解析式$\widehat{y}$=cx2+d作为蔬菜农药残量$\widehat{y}$与用水量x的回归方程,令ω=x2,计算平均值$\overline{ω}$和$\overline{y}$,完成如下表格,求出$\widehat{y}$与x回归方程.(c,d精确到0.01)
(Ⅲ)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时对人体无害,为了放心食用该蔬菜,请估计需要多少千克的清水洗一千克蔬菜?(精确到0.1,参考数据$\sqrt{5}$≈2.236).
(附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中系数计算公式分别为:
$\widehat{b}$=$\frac{\sum_{i-1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.)
 菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,使用时需要用清水清洗干净,如表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的统计表:
菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,使用时需要用清水清洗干净,如表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的统计表:| x | 1 | 2 | 3 | 4 | 5 |
| y | 58 | 54 | 39 | 29 | 10 |
(Ⅱ)若用解析式$\widehat{y}$=cx2+d作为蔬菜农药残量$\widehat{y}$与用水量x的回归方程,令ω=x2,计算平均值$\overline{ω}$和$\overline{y}$,完成如下表格,求出$\widehat{y}$与x回归方程.(c,d精确到0.01)
| ω | 1 | 4 | 9 | 16 | 25 |
| y | 58 | 54 | 39 | 29 | 10 |
| ωi-$\overline{ω}$ | |||||
| yi-$\overline{y}$ |
(附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中系数计算公式分别为:
$\widehat{b}$=$\frac{\sum_{i-1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.)
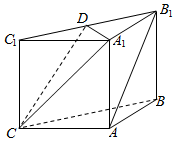 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.