题目内容
1.过双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的右焦点F的直线l与双曲线C交于M,N两点,A为双曲线的左焦点,若直线AM与直线AN的斜率k1,k2满足k1+k2=2,则直线l的方程是( )| A. | y=2(x-3) | B. | y=-2(x-3) | C. | y=$\frac{1}{2}$(x-3) | D. | y=-$\frac{1}{2}$(x-3) |
分析 设出直线方程与双曲线方程联立,利用韦达定理及k1+k2=2,求直线l的斜率,即可求出直线l的方程.
解答 解:设直线方程为l:y=k(x-3),M(x1,y1),N(x2,y2)
联立方程组得(5-4k2)x2+24k2x-36k2-20=0
∴x1+x2=-$\frac{24{k}^{2}}{5-4{k}^{2}}$,x1x2=$\frac{-36{k}^{2}-20}{5-4{k}^{2}}$
∴k1+k2=$\frac{{y}_{1}}{{x}_{1}+3}$+$\frac{{y}_{2}}{{x}_{2}+3}$=$\frac{2k({x}_{1}{x}_{2}-9)}{{x}_{1}{x}_{2}+3({x}_{1}+{x}_{2})+9}$=2
代入解得k=-2,
∴直线l的方程是y=-2(x-3).
故选:B.
点评 本题考查双曲线的几何性质,考查双曲线的标准方程,考查直线与双曲线的位置关系,考查韦达定理的运用,正确运用韦达定理是关键.

练习册系列答案
相关题目
10.函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)一个周期的图象如图所示,则( )
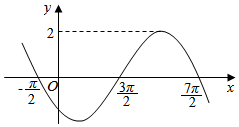

| A. | A=2,ω=2,φ=$\frac{3π}{4}$ | B. | A=2,ω=2,φ=$\frac{5π}{4}$ | C. | A=2,ω=$\frac{1}{2}$,φ=$\frac{3π}{4}$ | D. | A=2,ω=$\frac{1}{2}$,φ=$\frac{5π}{4}$ |
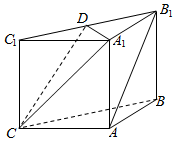 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点. 如图,点D是△ABC的边BC上一点,且AC=$\sqrt{3}$AD,$\sqrt{3}$CD=2AC,CD=2BD.
如图,点D是△ABC的边BC上一点,且AC=$\sqrt{3}$AD,$\sqrt{3}$CD=2AC,CD=2BD.