题目内容
16．某年高考中，某省10万考生在满分为150分的数学考试中，成绩分布近似服从正态分布N（110，100），则分数位于区间（130，150]分的考生人数近似为（ ）（已知若X～N（μ，σ2），则P（μ-σ＜X＜μ+σ）=0.6826，P（μ-2σ＜X＜μ+2σ）=0.9544，P（μ-3σ＜X＜μ+3σ）=0.9974．
| A． | 1140 | B． | 1075 | C． | 2280 | D． | 2150 |
分析 利用对称性先计算出P（X＞130），再计算人数．
解答 解：∵成绩分布近似服从正态分布N（110，100），
∴μ=110，σ=10，
∴P（90＜X＜130）=0.9544，
∴P（X＞130）=$\frac{1}{2}$（1-0.9544）=0.0228，
∴分数位于区间（130，150]分的考生人数约为100000×0.0228=2280．
故选：C．
点评 本题考查了正态分布的特点，属于基础题．
练习册系列答案
相关题目
6．已知函数$f（x）=\left\{\begin{array}{l}a•{2^x}，x≥0\\{2^{-x}}，x＜0\end{array}\right.$（a∈R），若f（f（-1））=1，则a=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
，其中A的各位数字中，a1=1，且ak（k=2，3，4，5）为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$．记ξ=a1+a2+a3+a4+a5，当程序运行一次时：
11．对于函数y=sin（$\frac{13}{2}$π-x），下面说法中正确的是（ ）
| A． | 函数是周期为2π的偶函数 | B． | 函数是周期为π的偶函数 | ||
| C． | 函数是周期为2π的奇函数 | D． | 函数是周期为π的奇函数 |
1．已知集合A={x∈R|f（x）=log2（x-2）}，B={y∈R|y=log2（x-2）}，则A∩B=（ ）
| A． | （0，2） | B． | （0，2] | C． | [2，+∞） | D． | （2，+∞） |
8．阅读下面的程序框图，运行相应的程序，则输出的K和S的值分别为（ ）
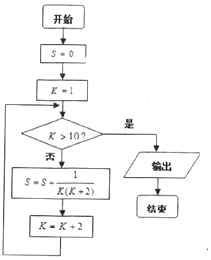
| A． | 9，$\frac{4}{9}$ | B． | 11，$\frac{5}{11}$ | C． | 11，$\frac{10}{11}$ | D． | 13，$\frac{12}{13}$ |