题目内容
已知圆G:x2+y2-2x-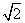 y=0经过椭圆
y=0经过椭圆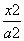 +
+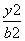 =1(a>b>0)的右焦点F及上顶点B.过椭圆外一点M(m,0)(m>a)作倾斜角为
=1(a>b>0)的右焦点F及上顶点B.过椭圆外一点M(m,0)(m>a)作倾斜角为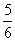 π的直线l交椭圆于C,D两点.
π的直线l交椭圆于C,D两点.
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的内部,求m的取值范围.
解 (1)∵圆G:x2+y2-2x-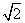 y=0经过点F,B,
y=0经过点F,B,
∴F(2,0),B(0,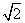 ),∴c=2,b=
),∴c=2,b=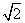 ,
,
∴a2=b2+c2=6,椭圆的方程为 +
+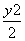 =1.
=1.
(2)由题意知直线l的方程为y=-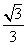 (x-m),m>
(x-m),m>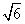 ,
,
由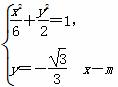
消去y,得2x2-2mx+(m2-6)=0.
由Δ=4m2-8(m2-6)>0,解得-2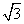 <m<2
<m<2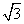 .
.
∵m>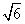 ,∴
,∴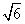 <m<2
<m<2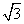 .设C(x1,y1),D(x2,y2),
.设C(x1,y1),D(x2,y2),
则x1+x2=m,x1x2=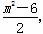 ,
,
∴y1y2=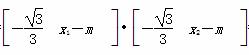 =
=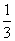 x1x2-
x1x2-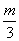 (x1+x2)+
(x1+x2)+ .
.
∵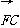 =(x1-2,y1).
=(x1-2,y1). 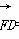 =(x2-2,y2),
=(x2-2,y2),
∴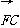 ·
·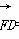 =(x1-2)(x2-2)+y1y2=
=(x1-2)(x2-2)+y1y2=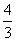 x1x2-
x1x2-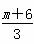 (x1+x2)+
(x1+x2)+ +4=
+4=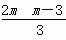 .
.
∵点F在圆E内部,∴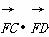 <0,
<0,
即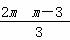 <0,解得0<m<3.
<0,解得0<m<3.
又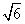 <m<2
<m<2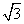 ,∴
,∴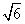 <m<3.
<m<3.
故m的取值范围是(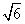 ,3).
,3).

练习册系列答案
相关题目
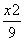 +
+ =1的离心率为
=1的离心率为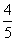 ,则k的值为( ).
,则k的值为( ). 或21 D.
或21 D.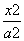 -
-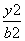 =1(a>0,b>0)和椭圆
=1(a>0,b>0)和椭圆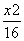 +
+ =1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为________.
=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为________.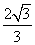 B.
B.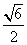 C.
C.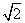 D.
D.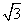
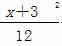 -
-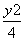 =1 B.
=1 B.  +
+