题目内容
14.在△ABC中,已知$\overrightarrow{BA}$=(2,4,0),$\overrightarrow{BC}$=(-1,3,0),则∠ABC=$\frac{π}{4}$.分析 利用向量夹角公式即可得出.
解答 解:∵cos∠ABC=$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BA}||\overrightarrow{BC}|}$=$\frac{-2+12+0}{\sqrt{{2}^{2}+{4}^{2}}\sqrt{(-1)^{2}+{3}^{2}}}$=$\frac{\sqrt{2}}{2}$,
∠ABC∈(0,π),
∴∠ABC=$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 本题考查了向量夹角公式、数量积运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
2.图(1)、图(2)、图(3)、图(4)分别包含1、5、13和25个互不重叠的单位正方形,按同样的方式构造图形,则第n个图包含( )个互不重叠的单位正方形.
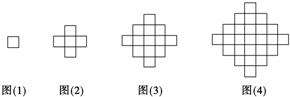

| A. | n2-2n+1 | B. | 2n2-2n+1 | C. | 2n2+2 | D. | 2n2-n+1 |
9.某程序框图如图所示,该程序执行后输出的y等于( )


| A. | 7 | B. | 15 | C. | 31 | D. | 63 |
4.若函数y=f(x)的图象与函数y=sin(x+$\frac{π}{4}$)的图象关于P($\frac{π}{2}$,0)对称,则f(x)解析式为( )
| A. | f(x)=sin(x-$\frac{π}{4}$) | B. | f(x)=-sin(x-$\frac{π}{4}$) | C. | f(x)=-cos(x+$\frac{π}{4}$) | D. | f(x)=cos(x-$\frac{π}{4}$) |