题目内容
19．已知Sn为等比数列{an}的前n项和，公比q=2，S99=154，则a3+a6+a9+…+a99=88．分析 公比q=2，S99=154，可得$\frac{{a}_{1}（1-{2}^{99}）}{1-2}$=154，可得${a}_{1}（{2}^{99}-1）$=154．又a3+a6+a9+…+a99=$\frac{{a}_{3}[（{2}^{3}）^{33}-1]}{{2}^{3}-1}$=$\frac{4{a}_{1}（{2}^{99}-1）}{7}$，代入即可得出．
解答 解：∵公比q=2，S99=154，∴$\frac{{a}_{1}（1-{2}^{99}）}{1-2}$=154，可得${a}_{1}（{2}^{99}-1）$=154．
则a3+a6+a9+…+a99=$\frac{{a}_{3}[（{2}^{3}）^{33}-1]}{{2}^{3}-1}$=$\frac{4{a}_{1}（{2}^{99}-1）}{7}$=$\frac{4}{7}×154$=88，
故答案为：88．
点评 本题考查了等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
13．
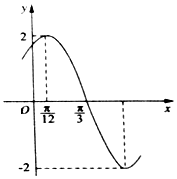已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，下列说法正确的是（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，下列说法正确的是（ ）| A． | 函数f（x）的图象关于直线x=-$\frac{2π}{3}$对称 | |
| B． | 函数f（x）的图象关于点（-$\frac{11π}{12}$，0）对称 | |
| C． | 若方程f（x）=m在[-$\frac{π}{2}$，0]上有两个不相等的实数根，则实数m∈（-2，-$\sqrt{3}$] | |
| D． | 将函数f（x）的图象向左平移$\frac{π}{6}$个单位可得到一个偶函数 |
8．$g（x）=x+\frac{1}{x}$上各点处的切线倾斜角为α，则α的取值范围（ ）
| A． | （0，π） | B． | $（{0，\frac{π}{4}}）$ | C． | $[{0，\frac{π}{4}}）∪（{\frac{3}{4}π，π}）$ | D． | $[{0，\frac{π}{4}}）∪（{\frac{π}{2}，π}）$ |