题目内容
设常数a∈R,集合A={x|(x-1)(x-a)≥0},B={x|(a-1)x≥a2-2a+1},若A∪B=R,则a的取值范围为( )
| A、(-∞,2) |
| B、(2,+∞) |
| C、[1,2] |
| D、(1,2) |
考点:集合关系中的参数取值问题
专题:计算题,集合
分析:当a>1时,代入解集中的不等式中,确定出A,求出满足两集合的并集为R时的a的范围;当a=1时,易得A=R,符合题意;当a<1时,同样求出集合A,列出关于a的不等式,求出不等式的解集得到a的范围.综上,得到满足题意的a范围.
解答:
解:当a>1时,A=(-∞,1]∪[a,+∞),B=[a-1,+∞),
若A∪B=R,则a-1≤1,
∴1<a≤2;
当a=1时,易得A=B=R,此时A∪B=R;
当a<1时,A=(-∞,a]∪[1,+∞),B=(-∞,a-1],
若A∪B=R,则a-1≥1,∴a≥2,矛盾;
综上,a的取值范围是[1,2].
故选C.
若A∪B=R,则a-1≤1,
∴1<a≤2;
当a=1时,易得A=B=R,此时A∪B=R;
当a<1时,A=(-∞,a]∪[1,+∞),B=(-∞,a-1],
若A∪B=R,则a-1≥1,∴a≥2,矛盾;
综上,a的取值范围是[1,2].
故选C.
点评:此题考查了并集及其运算,二次不等式,以及不等式恒成立的条件,熟练掌握并集的定义是解本题的关键.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
若α=390°,则角α的终边落在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
“D=
≠0”是“方程组
有唯一解”的( )
|
|
| A、充分不必要条件 |
| B、必要不充分条 |
| C、充要条件 |
| D、既不充分又不必要条件 |
设集合P={x|x2-2
x≤0},m=20.3,则下列关系中正确的是( )
| 3 |
| A、m⊆P | B、m∉P |
| C、{m}∈P | D、{m}?P |
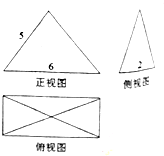 一个何体的三视图如图所示,其中正视图是底边长为6,腰长为5的等腰三角形,侧视图是底边长为2的等腰三角影,则该几何体的体积为( )
一个何体的三视图如图所示,其中正视图是底边长为6,腰长为5的等腰三角形,侧视图是底边长为2的等腰三角影,则该几何体的体积为( )| A、16 | B、24 | C、32 | D、48 |