题目内容
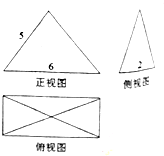一个何体的三视图如图所示，其中正视图是底边长为6，腰长为5的等腰三角形，侧视图是底边长为2的等腰三角影，则该几何体的体积为（ ）| A、16 | B、24 | C、32 | D、48 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知的三视图可得：该几何体是一个以俯视图为底面的四棱锥，分别求出底面面积和高，代入锥体体积公式，可得答案．
解答：
解：由已知的三视图可得：该几何体是一个以俯视图为底面的四棱锥，
棱锥的底面面积S=2×6=12，
棱锥的高h=
=4，
故棱锥的体积V=
Sh=16，
故选：A
棱锥的底面面积S=2×6=12，
棱锥的高h=
52-(
|
故棱锥的体积V=
| 1 |
| 3 |
故选：A
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
设常数a∈R，集合A={x|（x-1）（x-a）≥0}，B={x|（a-1）x≥a2-2a+1}，若A∪B=R，则a的取值范围为（ ）
| A、（-∞，2） |
| B、（2，+∞） |
| C、[1，2] |
| D、（1，2） |
已知异面直线a，b均与平面α相交，下列命题：
①存在直线m?α，使得m⊥a或m⊥b；
②存在直线m?α，使得m⊥a且m⊥b；
③存在直线m?α，使得m与a和b所成的角相等．
其中不正确的命题个数为（ ）
①存在直线m?α，使得m⊥a或m⊥b；
②存在直线m?α，使得m⊥a且m⊥b；
③存在直线m?α，使得m与a和b所成的角相等．
其中不正确的命题个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
已知cosαcosβ-sinαsinβ=0，那么sinαcosβ+cosαsinβ的值为（
| A、-1 | B、0 | C、1 | D、±1 |
与-460°角终边相同的角的集合（ ）
| A、{∂|∂=k•360°+460°（k∈Z）} |
| B、{∂|∂=k•360°+100°（k∈Z）} |
| C、{∂|∂=k•360°+260°（k∈Z）} |
| D、{∂|∂=k•360°-260°（k∈Z）} |