题目内容
已知长方体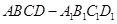 ,点
,点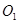 为
为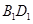 的中点.
的中点.
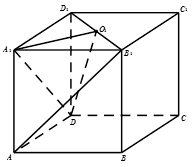
(1)求证: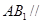 面
面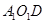 ;
;
(2)若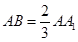 ,试问在线段
,试问在线段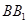 上是否存在点
上是否存在点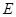 使得
使得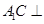
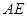 ,若存在求出
,若存在求出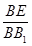 ,若不存在,说明理由.
,若不存在,说明理由.
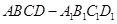 ,点
,点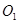 为
为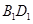 的中点.
的中点.
(1)求证:
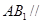 面
面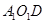 ;
;(2)若
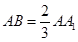 ,试问在线段
,试问在线段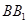 上是否存在点
上是否存在点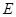 使得
使得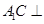
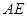 ,若存在求出
,若存在求出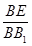 ,若不存在,说明理由.
,若不存在,说明理由.(1)证明详见解析;(2)存在,证明详见解析.
试题分析:(1)设
 与
与 的交点为
的交点为 ,由三角形的中位线可证
,由三角形的中位线可证 ∥AB1,,最后根据直线与平面平行的判定定理可证
∥AB1,,最后根据直线与平面平行的判定定理可证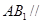 面
面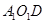 ;(2)假设存在
;(2)假设存在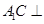
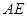 ,连结
,连结 交
交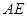 于点
于点 ,由直线与平面垂直的性质定理可得BC⊥AE,由直线与平面垂直的判定定理可得AE⊥平面
,由直线与平面垂直的性质定理可得BC⊥AE,由直线与平面垂直的判定定理可得AE⊥平面 ,即
,即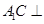
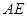 得证.根据两对应角相等,三角形相似证得Rt△ABE~Rt△A1AB,有相似比可证的
得证.根据两对应角相等,三角形相似证得Rt△ABE~Rt△A1AB,有相似比可证的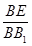 的比值.
的比值.试题解析:(1)证明:
连结
 交
交 于点
于点 ,所以
,所以 为
为 的中点,连结
的中点,连结
 在
在 中,
中,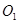 为
为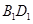 的中点
的中点 4分
4分
 面
面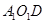 且
且 面
面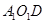

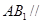 面
面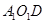 7分
7分
(2)若在线段
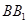 上存在点
上存在点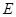 得
得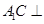
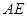 ,连结
,连结 交
交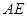 于点
于点
 面
面 且
且 面
面

又
 且
且 面
面
 面
面
 面
面
 10分
10分在
 和
和 中有:
中有:
 同理:
同理:
 12分
12分

 即在线段
即在线段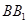 上存在点
上存在点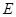 有
有 14分
14分

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 中,
中, 平面
平面 ,底面
,底面 ∥
∥ ,
, ,
, ,
,

 ⊥平面
⊥平面 ;
; 与
与 所成角的大小。
所成角的大小。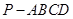 中,底面
中,底面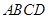 是矩形,四条侧棱长均相等且
是矩形,四条侧棱长均相等且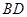 交
交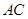 于点
于点 .
.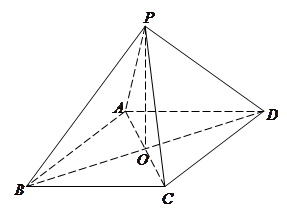
 ;
; .
.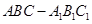 中,
中,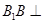 平面
平面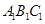 ,
,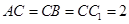 ,
, ,
, 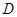 ,
, 分别是
分别是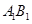 ,
,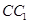 的中点.
的中点.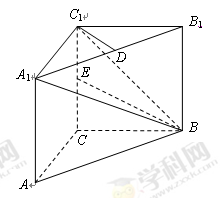
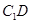 ∥平面
∥平面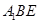 ;
;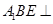 平面
平面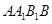 ;
;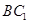 与平面
与平面 中,下列结论不正确的是 ( )
中,下列结论不正确的是 ( )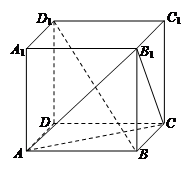
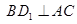
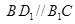
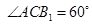
 是两个不同的平面,则下列命题中的真命题是 ( )
是两个不同的平面,则下列命题中的真命题是 ( ) 则
则
 ,则
,则
 ,
, 则
则 ,则
,则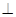 平面
平面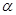 ,直线
,直线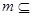 平面
平面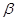 ,则下列四个结论:
,则下列四个结论: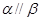 ,则
,则 ②若
②若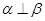 ,则
,则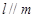
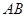 是
是 的直径,
的直径,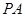 垂直于
垂直于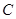 是圆周上不同于
是圆周上不同于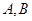 的任意一点,则图中直角三角形有 个.(要求:只需填直角三角形的个数,不需要具体指出三角形名称).
的任意一点,则图中直角三角形有 个.(要求:只需填直角三角形的个数,不需要具体指出三角形名称).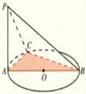
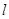 和平面
和平面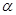 ,若
,若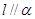 ,
,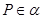 ,过点
,过点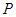 且平行于
且平行于