题目内容
15.已知函数f(x)=$\frac{{e}^{x}}{1+a{x}^{2}}$(1)当a=$\frac{4}{3}$时,求函数f(x)的极值;
(2)若f(x)为R上的单调函数,求实数a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(2)求出函数的导数,a=0时,不合题意,a≠0时,结合二次函数的性质求出a的范围即可.
解答 解:(1)a=$\frac{4}{3}$时,f(x)=$\frac{{e}^{x}}{1+{\frac{4}{3}x}^{2}}$,
f′(x)=$\frac{{3e}^{x}(2x-3)(2x-1)}{{(3+{4x}^{2})}^{2}}$,
令f′(x)>0,解得:x>$\frac{3}{2}$或x<$\frac{1}{2}$,
令f′(x)<0,解得:$\frac{1}{2}$<x<$\frac{3}{2}$,
∴f(x)在(-∞,$\frac{1}{2}$)递增,在($\frac{1}{2}$,$\frac{3}{2}$)递减,在($\frac{3}{2}$,+∞)递增,
∴f(x)极大值=f($\frac{1}{2}$)=$\frac{3\sqrt{e}}{4}$,f(x)极小值=f($\frac{3}{2}$)=$\frac{e\sqrt{e}}{4}$;
(2)f′(x)=$\frac{{e}^{x}({ax}^{2}-2ax+1)}{{(1+{ax}^{2})}^{2}}$,
a=0时,f′(x)>0,f(x)递增,符合题意,
a≠0时,若f(x)为R上的单调函数,
只需函数g(x)=ax2-2ax+1和x轴的交点最多是1个,
故△=4a2-4a≤0,解得:0≤a≤1,
综上:0≤a≤1.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及二次函数的性质,是一道中档题.

练习册系列答案
相关题目
4.已知全集U={0,1,2,3,4,5,6,7},集合A={0,1,3,6},集合B={2,5,6,7},则(∁UB)∪A=( )
| A. | {0,1,2,3,4,5,6,7} | B. | {6} | C. | {2,4,5,6,7} | D. | {0,1,3,4,6} |
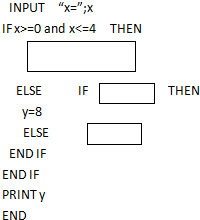 函数y=$\left\{\begin{array}{l}2x,0≤x≤4\\ 8,4<x≤8\\ 2(12-x),8<x≤12\end{array}$,填补方框内的内容完成函数的函数值的程序.
函数y=$\left\{\begin{array}{l}2x,0≤x≤4\\ 8,4<x≤8\\ 2(12-x),8<x≤12\end{array}$,填补方框内的内容完成函数的函数值的程序.