��Ŀ����
1����֪ij��ѧ�����Ŀư�ѧ������ѧ�������ˮƽ���Գɼ�����ͳ�������| x ���� y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
��1�����ڸ������У���ѧ�ɼ�����������30%����a��b��ֵ��
��2����֪a��8��b��6������ѧ�ɼ�ΪA�ȼ���������C�ȼ���������ĸ��ʣ�
���� ��1����Ƶ��=$\frac{Ƶ��}{����}$�������a��b��ֵ��
��2����14+a+28��10+b+34����a��b+2���ɴ������оٷ������������ʣ�
��� �⣺��1����Ƶ��=$\frac{Ƶ��}{����}$���õ�$\frac{14}{n}=0.07$��
���n=200��
��$\frac{14+a+28}{200}=0.3$�����a=18��
��14+a+28+40+36+8+10+b+34=200��
��b=12��
��2����a+b=30����a��8��b��6��
����14+a+28��10+b+34����a��b+2��
��a��b�������н��Ϊ��8��22������9��21������10��20������11��19������12��18������13��17����
��14��16������15��15������16��14������17��12������18��12������19��20������20��10������21��9������22��8������23��7������24��6����
��17�飬
����a��b+2����8�飬
����ѧ�ɼ�ΪA�ȼ���������C�ȼ���������ĸ���P=$\frac{8}{17}$��
���� ���⿼��Ƶ�ʷֲ�����Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�

��ϰ��ϵ�д�
 ����������ϵ�д�
����������ϵ�д�
�����Ŀ
14����֪˫���ߵķ���Ϊ$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0��������F1��б��Ϊ$\frac{\sqrt{3}}{3}$��ֱ�߽�˫���ߵ���֧�ڵ�P����y��ƽ���߶�F1P����˫���ߵ�������Ϊ��������
| A�� | $\sqrt{3}$ | B�� | $\sqrt{5}$+1 | C�� | $\sqrt{2}$ | D�� | 2+$\sqrt{3}$ |
15���뾶Ϊ2��ԲC��Բ���ڵ������ޣ�����ֱ��x=0��$x+y=2\sqrt{2}$�����У����Բ�ı�����Ϊ��������
| A�� | ��x-1��2+��y+2��2=4 | B�� | ��x-2��2+��y+2��2=2 | C�� | ��x-2��2+��y+2��2=4 | D�� | ��x-2$\sqrt{2}$��2+��y+2$\sqrt{2}$��2=4 |
6���ڡ�ABC�У�DΪ����������ƽ����һ�㣬��$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$����$\frac{{{S_{��BCD}}}}{{{S_{��ABD}}}}$=��������
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
13��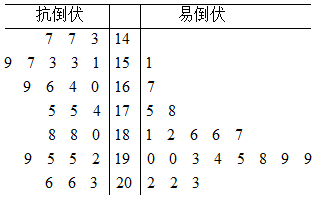 Ϊ�˴����ƶ����ս��ijƶ����ũ��Ժ���������ֲ������е��У�������Ч�ظ�������Ʒ�֣�Ϊũ���ṩ����֧Ԯ���ֶ���ѡ����һ�����ľ��߽���ͳ�ƣ���þ�Ҷͼ��ͼ����λ�����ף����辥�ߴ��ڻ����180��������Ϊ�߾����ף�����Ϊ�������ף�
Ϊ�˴����ƶ����ս��ijƶ����ũ��Ժ���������ֲ������е��У�������Ч�ظ�������Ʒ�֣�Ϊũ���ṩ����֧Ԯ���ֶ���ѡ����һ�����ľ��߽���ͳ�ƣ���þ�Ҷͼ��ͼ����λ�����ף����辥�ߴ��ڻ����180��������Ϊ�߾����ף�����Ϊ�������ף�
��1�����2��2�����������ж��Ƿ�����ڷ�������ʲ�����1%��ǰ���£���Ϊ�����������װ����йأ�
��2����i�����շֲ�����ķ�ʽ�������������У��������Ϳ����������г��9�����ף���ȡ��������������������ΪX����X�ķֲ��У��������������ʽ��ʾ��
��ii������Ƶ����Ϊ���ʣ��ӿ������������������������ȡ��50�꣬��ȡ���ĸ߾�������������ѧ�����ͷ���
�� ${{K}^2}=\frac{{n{{��ad-bc��}^2}}}{��a+b����c+d����a+c����b+d��}$������n=a+b+c+d��
 Ϊ�˴����ƶ����ս��ijƶ����ũ��Ժ���������ֲ������е��У�������Ч�ظ�������Ʒ�֣�Ϊũ���ṩ����֧Ԯ���ֶ���ѡ����һ�����ľ��߽���ͳ�ƣ���þ�Ҷͼ��ͼ����λ�����ף����辥�ߴ��ڻ����180��������Ϊ�߾����ף�����Ϊ�������ף�
Ϊ�˴����ƶ����ս��ijƶ����ũ��Ժ���������ֲ������е��У�������Ч�ظ�������Ʒ�֣�Ϊũ���ṩ����֧Ԯ���ֶ���ѡ����һ�����ľ��߽���ͳ�ƣ���þ�Ҷͼ��ͼ����λ�����ף����辥�ߴ��ڻ����180��������Ϊ�߾����ף�����Ϊ�������ף���1�����2��2�����������ж��Ƿ�����ڷ�������ʲ�����1%��ǰ���£���Ϊ�����������װ����йأ�
��2����i�����շֲ�����ķ�ʽ�������������У��������Ϳ����������г��9�����ף���ȡ��������������������ΪX����X�ķֲ��У��������������ʽ��ʾ��
��ii������Ƶ����Ϊ���ʣ��ӿ������������������������ȡ��50�꣬��ȡ���ĸ߾�������������ѧ�����ͷ���
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ��
��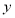 ����Լ������
����Լ������ ��
��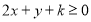 ���������ʵ��
���������ʵ��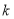 ��ȡֵ��ΧΪ ��
��ȡֵ��ΧΪ �� �ڵĺ���
�ڵĺ���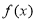 ����
���� ����
���� ʱ��
ʱ��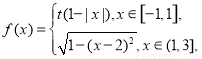 ��
�� ʱ������
ʱ������ �IJ���ʵ�����ĸ����ǣ� ��
�IJ���ʵ�����ĸ����ǣ� ��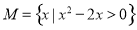 ������
������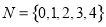 ����
����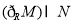 ���ڣ� ��
���ڣ� �� B��
B��
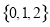 D��
D��