题目内容
7.若函数f(x)=$\sqrt{(-ax+1)}$在[-1,+∞)上有意义,则实数a的取值范围是[-1,0].分析 问题转化为-ax+1≥0在[-1,+∞)恒成立,通过讨论a的符号,求出a的范围即可.
解答 解:-ax+1≥0,ax≤1,x≥-1有意义,
a=0,则0≤1,成立,
a≠0则一定a<0,x≥$\frac{1}{a}$恒成立?$\frac{1}{a}$≤xmin=-1,
所以-1≥$\frac{1}{a}$,解得:a≥-1,
所以-1≤a≤0.
点评 本题考查了求函数的定义域问题,考查二次根式的性质,是一道基础题.

练习册系列答案
相关题目
18.若集合M={-2,-1,0,1,2},N={x|x2<3},则M∩N等于( )
| A. | ∅ | B. | {-1,1} | C. | {-2,2} | D. | {-1,0,1} |
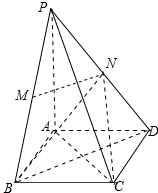 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点