题目内容
17.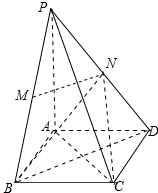 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点(1)证明:MN∥平面ABCD;
(2)证明:BD⊥平面PAC;
(3)求三棱锥C-BDN的体积.
分析 (1)由M,N分别是PB,PD的中点,可得MN∥BD,即可证明MN∥平面ABCD.
(2)利用线面垂直的判定定理证明BD⊥平面PAC;
(3)三棱锥C-BDN的体积=三棱锥N-CBD的体积,即可求三棱锥C-BDN的体积.
解答 (1)证明:因为:M,N分别是PB,PD的中点,
所以:MN是△PBD的中位线,
所以:MN∥BD,
又因为:MN?面ABCD,BD?面ABCD,
所以:MN∥平面ABCD.
(2)证明:∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD,
∵ABCD边长为2$\sqrt{3}$菱形,
∴BD⊥AC,
∵PA∩AC=A,
∴BD⊥平面PAC;
(3)解:三棱锥C-BDN的体积=三棱锥N-CBD的体积=$\frac{1}{3}×\frac{1}{2}×2\sqrt{3}×2\sqrt{3}×sin120°×\sqrt{6}$=$\frac{3\sqrt{2}}{2}$.
点评 本题主要考查了直线与平面平行、垂直的判定,棱柱、棱锥、棱台的体积的求法,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
