题目内容
若函数f(x)满足对于x∈[n,m](m>n)时有
≤f(x)≤km恒成立,则称函数f(x)在区间[n,m](m>n)上是“被k限制”的,若函数f(x)=x2-ax+a2在区间[
,a](a>0)上是“被2限制”的,则实数a的取值范围是( )
| n |
| k |
| 1 |
| a |
A、(1,
| |||||
B、(1,
| |||||
| C、(1,2] | |||||
D、[
|
考点:函数的值域
专题:函数的性质及应用,不等式的解法及应用
分析:根据题意得a>1;求出x∈[
,a]时,f(x)的取值范围①,再由
≤f(x)≤2a②,
由①②得不等式组,求出a的取值范围.
| 1 |
| a |
| 1 |
| 2a |
由①②得不等式组,求出a的取值范围.
解答:
解:根据题意,∵a>0,且
<a,∴a>1;
f(x)=x2-ax+a2=(x-
)2+
≥
,
(Ⅰ)当
∈[
,a],即a≥
时,在x=
时,f(x)取得最小值
;
又∵(
-
)-(a-
)=-
<0,
∴x=a时,f(x)取得最大值a2;
∴f(x)的取值范围是[
,a2]①;
又∵
≤f(x)≤2a②;
∴
,
解得
≤a≤2;
∴
≤a≤2;
(Ⅱ)当
<
,即1<a<
时,
f(x)在[
,a]上是增函数,
∴f(x)的最小值是f(
)=
-1+a2,最大值是f(a)=a2;
∴f(x)的值域是[
-1+a2,a2]③;
又∵
≤f(x)≤2a②;
∴
;
解得1<a<
;
综上,a的取值范围是{a|1<a≤2}.
故选:C.
| 1 |
| a |
f(x)=x2-ax+a2=(x-
| a |
| 2 |
| 3a2 |
| 4 |
| 3a2 |
| 4 |
(Ⅰ)当
| a |
| 2 |
| 1 |
| a |
| 2 |
| a |
| 2 |
| 3a2 |
| 4 |
又∵(
| a |
| 2 |
| 1 |
| a |
| a |
| 2 |
| 1 |
| a |
∴x=a时,f(x)取得最大值a2;
∴f(x)的取值范围是[
| 3a2 |
| 4 |
又∵
| 1 |
| 2a |
∴
|
解得
| 3 |
| ||
∴
| 2 |
(Ⅱ)当
| a |
| 2 |
| 1 |
| a |
| 2 |
f(x)在[
| 1 |
| a |
∴f(x)的最小值是f(
| 1 |
| a |
| 1 |
| a2 |
∴f(x)的值域是[
| 1 |
| a2 |
又∵
| 1 |
| 2a |
∴
|
解得1<a<
| 2 |
综上,a的取值范围是{a|1<a≤2}.
故选:C.
点评:本题考查了新定义的问题以及函数的应用问题,解题时应根据题意,求出函数f(x)的取值范围,列不等式组,求出a的取值范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设复数ω1=-
+
i,ω2=cos
+isin
,若z=ω1•ω2,则复数z的虚部为( )
| 1 |
| 2 |
| ||
| 2 |
| π |
| 12 |
| π |
| 12 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
sin(-
)的值等于( )
| 5π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
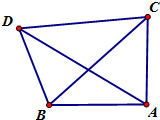 A,B两地相距200m,且A地在B地的正东方.一人在A地测得建筑C在正北方,建筑D在北偏西60°;在B地测得建筑C在北偏东45°,建筑D在北偏西15°,则两建筑C和D之间的距离为( )
A,B两地相距200m,且A地在B地的正东方.一人在A地测得建筑C在正北方,建筑D在北偏西60°;在B地测得建筑C在北偏东45°,建筑D在北偏西15°,则两建筑C和D之间的距离为( )A、200
| ||
B、100
| ||
C、100
| ||
D、100(
|
阅读如图所示的程序框图,运行相应的程序,输出的结果k=( )


| A、4 | B、5 | C、6 | D、7 |
已知a>0且a≠1,则ab>1是(a-1)b>0的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如果复数
(b∈R)的实部和虚部互为相反数,那么b等于( )
| 2-bi |
| i |
A、
| ||
B、-
| ||
| C、-2 | ||
| D、2 |