题目内容
一个球面上有三个点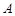 、
、 、
、 ,若
,若 ,
,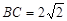 ,球心到平面
,球心到平面 的距离为1,则球的表面积为( )
的距离为1,则球的表面积为( )
A.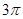 | B. | C. | D.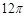 |
D
解析试题分析:由“∠BAC=90°,AB=AC=2,”得到BC即为A、B、C三点所在圆的直径,取BC的中点M,连接OM,则OM即为球心到平面ABC的距离,在Rt△OMB中,OM=1,MB= ,即可求球的半径,然后求出球的表面积. 解:如图所示:
,即可求球的半径,然后求出球的表面积. 解:如图所示:
取BC的中点M,则球面上A、B、C三点所在的圆即为⊙M,连接OM,则OM即为球心到平面ABC的距离,
在Rt△OMB中,OM=1,MB= ,∴OA=
,∴OA= ,即球球的半径为
,即球球的半径为 所以球的表面积为:4π(
所以球的表面积为:4π( )2=12π.故选D.
)2=12π.故选D.
考点:点到平面的距离
点评:本题考查球的有关计算问题,点到平面的距离,体积的求法,是基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
关于两条不同的直线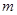 ,
, 与两个不同的平面
与两个不同的平面 ,
, ,下列正确的是( )
,下列正确的是( )
A. 且 且 ,则 ,则 |
B. 且 且 ,则 ,则 |
C. 且 且 ,则 ,则 |
D. 且 且 ,则 ,则 |
若 是空间中互不相同的直线,
是空间中互不相同的直线,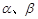 是不重合的两平面,则下列命题中为真命题的是( )
是不重合的两平面,则下列命题中为真命题的是( )
A.若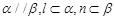 ,则 ,则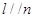 | B.若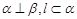 ,则 ,则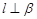 |
C.若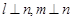 ,则 ,则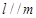 | D.若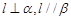 ,则 ,则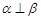 |
如图,在正方体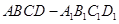 中,
中,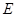 、
、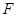 分别为棱
分别为棱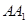 、
、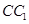 的中点,则在空间中与直线
的中点,则在空间中与直线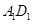 、
、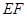 、CD都相交的直线有
、CD都相交的直线有
| A.1条 | B.2条 | C.3条 | D.无数条 |
四面体SABC中,E,F,G分别是棱SC,AB,SB的中点,若异面直线SA与BC所成的角等于45º,则∠EGF等于( )
| A.90º | B.60º或120º | C.45º | D.45º或135º |
在正三棱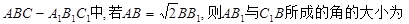 ( )
( )
A.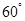 | B.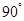 | C.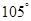 | D.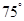 |
设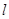 为直线,
为直线, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
 ABC的边AB,BC,CA的中点,O是△ABC的重心,则
ABC的边AB,BC,CA的中点,O是△ABC的重心,则 ( )
( )




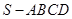 的底面边长为
的底面边长为 ,高
,高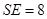 ,点
,点 在高
在高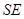 上,且
上,且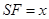 ,记过点
,记过点 的球的半径为
的球的半径为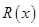 ,则函数
,则函数