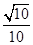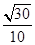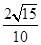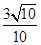题目内容
如图,在正方体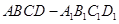 中,
中,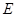 、
、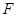 分别为棱
分别为棱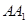 、
、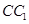 的中点,则在空间中与直线
的中点,则在空间中与直线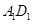 、
、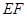 、CD都相交的直线有
、CD都相交的直线有
| A.1条 | B.2条 | C.3条 | D.无数条 |
D
解析试题分析:如图,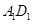 上任意取一点
上任意取一点 ,作平面
,作平面 ,注意
,注意 在此平面的两侧,
在此平面的两侧, 与此平面交于
与此平面交于 ,
, 与
与 不平行,即直线
不平行,即直线 与三条直线
与三条直线 都相交,而
都相交,而 是
是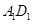 上任意一点,所以,这种直线有无数条。
上任意一点,所以,这种直线有无数条。
考点:空间直线间的位置关系
点评:本题要求学生要有一定的空间想象能力,学生在求解时的入手点不易找到,有一定难度

练习册系列答案
相关题目
用 、
、 、
、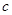 表示三条不同的直线,
表示三条不同的直线,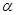 表示平面,给出下列命题:
表示平面,给出下列命题:
①若 ∥
∥ ,
, ∥
∥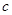 ,则
,则 ∥
∥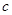 ; ②若
; ②若 ⊥
⊥ ,
, ⊥
⊥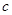 ,则
,则 ⊥
⊥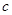 ;
;
③若 ∥
∥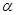 ,
, ∥
∥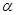 ,则
,则 ∥
∥ ; ④若
; ④若 ⊥
⊥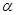 ,
, ⊥
⊥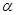 ,则
,则 ∥
∥ .
.
| A.①② | B.②③ | C.①④ | D.③④ |
在棱长为2的正方体中,点E,F分别是棱AB,BC的中点,则点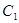 到平面
到平面 的距离等于( )
的距离等于( )
A.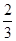 | B.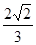 | C.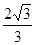 | D. |
一个球面上有三个点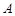 、
、 、
、 ,若
,若 ,
,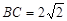 ,球心到平面
,球心到平面 的距离为1,则球的表面积为( )
的距离为1,则球的表面积为( )
A.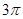 | B. | C. | D.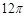 |
长方体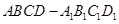 中,
中,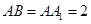 ,
,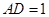 ,
,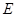 为
为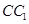 的中点,则异面直线
的中点,则异面直线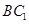 与
与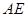 所成角的余弦值为
所成角的余弦值为
A.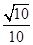 | B.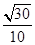 | C.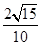 | D.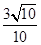 |
如图所示,正方体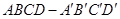 的棱长为1,O是平面
的棱长为1,O是平面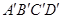 的中心,则O到平面
的中心,则O到平面 的距离是( )
的距离是( )
A.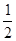 | B.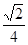 | C.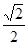 | D.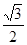 |
 的边长为
的边长为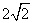 ,将
,将 沿对角线
沿对角线 折起,使平面
折起,使平面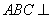 平面
平面 ,得到如图所示的三棱锥
,得到如图所示的三棱锥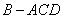 .若
.若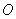 为
为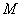 ,
, 分别为线段
分别为线段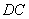 ,
,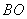 上的动点(不包括端点),且
上的动点(不包括端点),且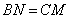 .设
.设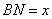 ,则三棱锥
,则三棱锥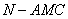 的体积
的体积 的函数图象大致是
的函数图象大致是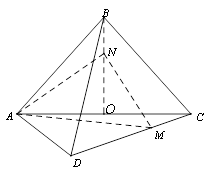



 且
且 ,则
,则 ;②若
;②若 且
且 ,则
,则 ;
; 且
且 且
且 ①②
①②  ③④
③④  ①④
①④  ②③
②③