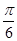题目内容
关于两条不同的直线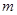 ,
, 与两个不同的平面
与两个不同的平面 ,
, ,下列正确的是( )
,下列正确的是( )
A. 且 且 ,则 ,则 |
B. 且 且 ,则 ,则 |
C. 且 且 ,则 ,则 |
D. 且 且 ,则 ,则 |
C
解析试题分析:根据空间中面面平行及线面平行的性质,我们易判断A的对错,根据线线垂直的判定方法,我们易判断出B的真假;根据空间中直线 与直线垂直的判断方法,我们可得到C的正误;根据线面平行及线面平行的性质,我们易得到D的对错,进而得到结论.解:若m∥α,n∥β且α∥β,则m与n可能平行与可能异面,故A错误;若m⊥α,n⊥β且α⊥β,则m⊥n,故B错误;当n∥β且α∥β时,存在直线l?α,使l∥n,又由m⊥α,故m⊥l,则m⊥n,故C正确;若n⊥β且α⊥β,则n∥α或n?α,若m∥α,则m与n可能平行,也可能垂直,也可能相交,故D错误;故选C
考点:空间中直线与直线之间的位置关系
点评:本题考查的知识点是空间中直线与直线之间的位置关系,熟练掌握空间中线与面之间位置关系的定义及判定方法是解答本题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
对于不重合的直线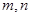 和不重合的平面
和不重合的平面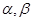 ,下列命题错误的是( )
,下列命题错误的是( )
A.若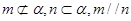 ,则 ,则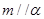 | B.若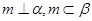 ,则 ,则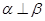 |
C.若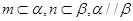 ,则 ,则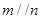 | D.若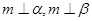 ,则 ,则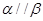 |
若 是空间三条不同的直线,
是空间三条不同的直线, 是空间中不同的平面,则下列命题中不正确的是( )
是空间中不同的平面,则下列命题中不正确的是( )
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.当 且 且 是 是 在 在 内的射影,若 内的射影,若 ,则 ,则 |
D.当 且 且 时,若 时,若 ,则 ,则 |
已知 是不同的两条直线,
是不同的两条直线,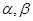 是不重合的两个平面,则下列命题中为真命题的是( )
是不重合的两个平面,则下列命题中为真命题的是( )
A.若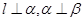 ,则 ,则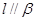 |
B.若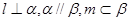 ,则 ,则 |
C.若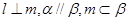 ,则 ,则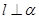 |
D.若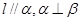 ,则 ,则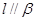 |
如图,正方体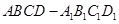 的棱长为1,线段
的棱长为1,线段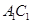 上有两个动点
上有两个动点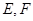 ,且
,且 ;则下列结论错误的是( )
;则下列结论错误的是( )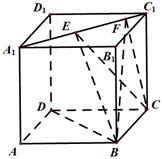
A.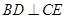 |
B.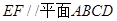 |
C.三棱锥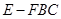 的体积为定值 的体积为定值 |
D.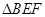 的面积与 的面积与 的面积相等 的面积相等 |
在棱长为2的正方体中,点E,F分别是棱AB,BC的中点,则点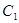 到平面
到平面 的距离等于( )
的距离等于( )
A.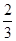 | B.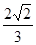 | C.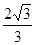 | D. |
一个球面上有三个点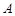 、
、 、
、 ,若
,若 ,
,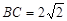 ,球心到平面
,球心到平面 的距离为1,则球的表面积为( )
的距离为1,则球的表面积为( )
A.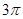 | B. | C. | D.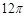 |

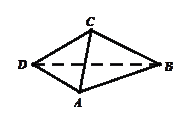
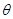 ,现沿对角线BD折成60°的二面角,翻折后
,现沿对角线BD折成60°的二面角,翻折后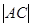 =
= a,则锐角A是( )
a,则锐角A是( )