题目内容
20. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率 e=$\frac{4}{5}$,且经过点(0,3),左右焦点分别为F1,F2,
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率 e=$\frac{4}{5}$,且经过点(0,3),左右焦点分别为F1,F2,(1)求椭圆C的方程;
(2)过F1作直线l与椭圆C交于A、B两点,求△ABF2的面积S的最大值,并求出S取最大值时直线l的方程.
分析 (1)利用椭圆C的离心率,且椭圆经过点(0,3)建立方程,求出几何量,即可求椭圆C的标准方程;
(2)由椭圆方程可得左、右两个焦点分别为F1(-4,0),F2(4,0).设直线l的方程为my=x+4.与椭圆方程联立消去x可得根与系数的关系,利用△ABF2面积S=$\frac{1}{2}$|F1F2||y1-y2|,可得关于m的表达式,再利用基本不等式即可得出.
解答 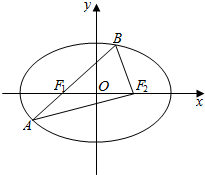 解:(1)椭圆的焦点在x轴上,
解:(1)椭圆的焦点在x轴上,
∵椭圆过点A(0,3),离心率e=$\frac{4}{5}$,
∴$\frac{9}{{b}^{2}}$=1,$\frac{c}{a}$=$\frac{4}{5}$,
∵c2=a2-b2.
∴a2=25,b2=9,
∴椭圆方程为$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1.
(2)由椭圆方程可得a2=25,b2=9,c=4,
左、右两个焦点分别为F1(-4,0),F2(4,0).
设直线l的方程为my=x+4,代入椭圆方程整理可得:(25+9m2)y2-72my-81=0.
∴y1+y2=$\frac{72m}{25+9{m}^{2}}$,y1y2=-$\frac{81}{25+9{m}^{2}}$.
∴|y1-y2|=$\sqrt{{(y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{(\frac{72m}{25+9{m}^{2}})^{2}+\frac{324}{25+9{m}^{2}}}$=90$\sqrt{\frac{1+{m}^{2}}{({25+9{m}^{2})}^{2}}}$.
∴△ABF2面积S=$\frac{1}{2}$|F1F2||y1-y2|=$\frac{1}{2}$×8×90$\sqrt{\frac{1+{m}^{2}}{({25+9{m}^{2})}^{2}}}$=360$\sqrt{\frac{1+{m}^{2}}{({25+9{m}^{2})}^{2}}}$,
令t=1+m2(t≥1),则S=360$\sqrt{\frac{t}{(16+9t)^{2}}}$=360$\sqrt{\frac{1}{81t+\frac{256}{t}+288}}$,
由81t+$\frac{256}{t}$≥2$\sqrt{81t•\frac{256}{t}}$=288,当且仅当t=$\frac{16}{9}$取得等号.
△ABF2面积S取得最大值360×$\sqrt{\frac{1}{576}}$=15.
即当m=±$\frac{\sqrt{7}}{3}$时,△ABF2面积S取得最大15.
点评 本题考查直线与圆锥曲线的位置关系及椭圆方程的求解,考查函数思想在解决问题中的应用,注意运用椭圆的定义和转化为方程联立可得根与系数的关系,考查了推理能力与计算能力,属于中档题.

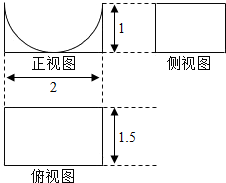
| A. | 6-$\frac{3π}{4}$ | B. | 6-$\frac{3π}{2}$ | C. | 3-$\frac{3π}{2}$ | D. | 3-$\frac{3π}{4}$ |
| A. | 点P在椭圆C外 | B. | 点P在椭圆C内 | ||
| C. | 点P在椭圆C上 | D. | 点P与椭圆C的位置关系不能确定 |
 已知点P为矩形ABCD所在平面外一点,AB=3,BC=2,平面PAB∩平面PCD=l.
已知点P为矩形ABCD所在平面外一点,AB=3,BC=2,平面PAB∩平面PCD=l.