题目内容
设集合A={x|2≤x≤5}，B={x|m+1≤x≤2m-1}，若B⊆A，求实数m的取值范围．
考点：集合的包含关系判断及应用
专题：集合
分析：分集合B为空集和非空集合两种情况讨论，然后根据集合间的包含关系分别列出不等式组求解，最后两种情况下的结果取并集．
解答：
解：由题意得：
当m+1＞2m-1，即m＜2时，集合B=∅，结论显然成立；
当B≠∅时，只需
成立，解得2≤m≤3．
综上，所求m的范围是（-∞，3]．
当m+1＞2m-1，即m＜2时，集合B=∅，结论显然成立；
当B≠∅时，只需
|
综上，所求m的范围是（-∞，3]．
点评：本题考查了集合的包含关系以及应用，主要是根据它们的自己关系构造出所求字母的不等式（组）求解，注意不要忘了空集的情况．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
若
=
，则tan2α=（ ）
| 1+cos2α |
| sin2α |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
一空间几何体的三视图如图所示，则该几何体的体积为（ ）
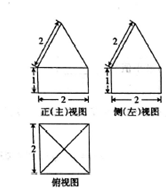
A、2+2
| ||||
B、4+2
| ||||
C、2+
| ||||
D、4+
|
三角函数f（x）=asinx-bcosx，若f（
-x）=f（
+x），则直线ax-by+c=0的倾斜角为（ ）
| π |
| 4 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设全集U={x|x≥3，x∈N}，集合A={x|x2≥10，x∈N}．则∁UA=（ ）
| A、∅ |
| B、{3} |
| C、{10} |
| D、{3，4，5，6，7，8，9} |