题目内容
已知函数f（x）=1-x2（x≥0）．
（1）求函数y=f-1（x）的解析式；
（2）求函数y=f（x）与y=f-1（x）的图象的公共点的坐标．
（1）求函数y=f-1（x）的解析式；
（2）求函数y=f（x）与y=f-1（x）的图象的公共点的坐标．
考点：反函数,函数解析式的求解及常用方法,函数的图象
专题：函数的性质及应用
分析：（1）根据反函数的定义求出反函数即可
（2）联立y=f（x）与y=f-1（x）得关于x，y的方程组，解得即可
（2）联立y=f（x）与y=f-1（x）得关于x，y的方程组，解得即可
解答：
解：（1）∵y=1-x2（x≥0），
∴x2=1-y，
∴x=
，y≤1，
∴y=f-1（x）=
，x≤1，
（2）联立y=f（x）与y=f-1（x）得
，0≤x≤1
解得
或
或
，
∴公共点的坐标为（0，1），（1，0），（
，
）
∴x2=1-y，
∴x=
| 1-y |
∴y=f-1（x）=
| 1-x |
（2）联立y=f（x）与y=f-1（x）得
|
解得
|
|
|
∴公共点的坐标为（0，1），（1，0），（
-1+
| ||
| 2 |
-1+
| ||
| 2 |
点评：本题考查了反函数的定义和图象的公共点的坐标问题，属于基础题
练习册系列答案
相关题目
若sinθ+cosθ=
，则tan（θ+
）的值是（ ）
| 2 |
| π |
| 3 |
| A、1 | ||
B、-
| ||
C、-1+
| ||
D、-
|
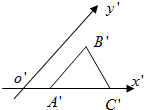如图是水平放置的△ABC的直观图，A′B′∥y′轴，A′B′=A′C′，则△ABC是（ ）| A、等边三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
某市中学生田径运动会总分获得冠、亚、季军的代表队人数如图表中所示，大会组委会为使颁奖仪式有序进行，气氛活跃，在颁奖过程中穿插抽奖活动，并用分层抽样方法从三个代表队中抽取16人在前排就座，其中亚军队有5人．