题目内容
6.已知函数$f(x)=ln(\sqrt{{x^2}+1}-x)$,对任意m∈[-3,3],不等式f(1-mx)+f(2x)<0恒成立,则实数x的取值范围为(-$\frac{1}{5}$,1).分析 根据函数表达式判断函数为奇函数,在判断函数的单调性,把函数变形为$f(x)=ln(\sqrt{{x^2}+1}-x)$=-ln$(\sqrt{{x}^{2}+1}+x)$,显然可知函数递减,
不等式f(1-mx)+f(2x)<0恒成立,可转化为xm-2x-1<0恒成立,可看成关于m的一次函数,利用一次函数性质解题即可.
解答 解:$f(x)=ln(\sqrt{{x^2}+1}-x)$,定义域为R,
∴f(-x)=ln($\sqrt{{x}^{2}+1}+x$)=ln$\frac{1}{\sqrt{{x}^{2}+1}-x}$=-f(x),
∴函数为奇函数,
∵$f(x)=ln(\sqrt{{x^2}+1}-x)$=-ln$(\sqrt{{x}^{2}+1}+x)$,
∴函数为减函数,
∵不等式f(1-mx)+f(2x)<0恒成立,
∴2x>mx-1恒成立,
∴xm-2x-1<0恒成立,
∴-3x-1-2x<0且3x-1-2x<0,
∴-$\frac{1}{5}$<x<1.
点评 考查了抽象函数的奇偶性和单调性和利用一次函数性质解决恒成立问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.数列{an}是等差数列,且a1>0,若a1008+a1009>0,a1008•a1009<0同时成立,则使得Sn>0成立的n的最大值为( )
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
14.等差数列{an}中,a1+a7=8,则a2+a4+a6=( )
| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
18.如图是一个算法的程序框图,当输入x的值为3时,输出y的结果恰好是$\frac{1}{3}$,则?处的关系式可以是( )
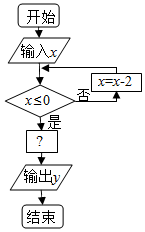

| A. | y=x2 | B. | y=3-x | C. | y=3x | D. | y=x${\;}^{\frac{1}{3}}$ |
16.若(z-1)2=-1,则z的值为( )
| A. | 1+i | B. | 1±i | C. | 2+i | D. | 2±i |