题目内容
12.已知函数f(x)=lnx-(x-1)(a为常数).(1)求函数f(x)的极值;
(2)试证明:对任意的n∈N*,都有ln(1+$\frac{1}{n}$)$<\frac{1}{n}$.
分析 (1)先确定函数f(x)的定义域,再求导f′(x)=$\frac{1}{x}$-1=$\frac{1-x}{x}$,从而判断函数的单调性与极值;
(2)由(1)知当x∈(1,2]时,f(x)<f(1)=0,即lnx<x-1,再令x=1+$\frac{1}{n}$即可.
解答 解:(1)函数f(x)=lnx-(x-1)的定义域为(0,+∞),
f′(x)=$\frac{1}{x}$-1=$\frac{1-x}{x}$,
故当x∈(0,1)时,f′(x)>0;
当x∈(1,+∞)时,f′(x)<0;
故f(x)在x=1处有极大值f(1)=0-(1-1)=0;
(2)证明:由(1)知,
当x∈(1,2]时,f(x)<f(1)=0,
即lnx<x-1,
令x=1+$\frac{1}{n}$,则
ln(1+$\frac{1}{n}$)<1+$\frac{1}{n}$-1,
即ln(1+$\frac{1}{n}$)<$\frac{1}{n}$,
故对任意的n∈N*,都有ln(1+$\frac{1}{n}$)$<\frac{1}{n}$.
点评 本题考查了导数的综合应用,同时考查了换元法的应用.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
3.复数$z=\frac{1-3i}{1+i}$的模是( )
| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
20. 如图中的曲线是指数函数的图象,已知a的值分别取$\sqrt{2}$,$\frac{4}{3}$,$\frac{3}{10}$,$\frac{1}{5}$,则相应于曲线C1,C2,C3,C4的a依次为( )
如图中的曲线是指数函数的图象,已知a的值分别取$\sqrt{2}$,$\frac{4}{3}$,$\frac{3}{10}$,$\frac{1}{5}$,则相应于曲线C1,C2,C3,C4的a依次为( )
 如图中的曲线是指数函数的图象,已知a的值分别取$\sqrt{2}$,$\frac{4}{3}$,$\frac{3}{10}$,$\frac{1}{5}$,则相应于曲线C1,C2,C3,C4的a依次为( )
如图中的曲线是指数函数的图象,已知a的值分别取$\sqrt{2}$,$\frac{4}{3}$,$\frac{3}{10}$,$\frac{1}{5}$,则相应于曲线C1,C2,C3,C4的a依次为( )| A. | $\frac{4}{3}$,$\sqrt{2}$,$\frac{1}{5}$,$\frac{3}{10}$ | B. | $\sqrt{2}$,$\frac{4}{3}$,$\frac{3}{10}$,$\frac{1}{5}$ | C. | $\frac{3}{10}$,$\frac{1}{5}$,$\sqrt{2}$,$\frac{4}{3}$ | D. | $\frac{1}{5}$,$\frac{3}{10}$,$\frac{4}{3}$,$\sqrt{2}$ |
17.在△ABC中,若cosA=$\frac{4}{5}$,tan(A-B)=-$\frac{1}{2}$,则tanB=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | 3 |
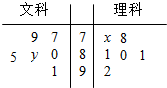 某中学从文、理科实验班中各选6名同学去参加复旦大学自主招生考试,其数学成绩茎叶图如图,其中文科生的成绩的众数为85,理科生成绩平均数为81,则x•y的值为( )
某中学从文、理科实验班中各选6名同学去参加复旦大学自主招生考试,其数学成绩茎叶图如图,其中文科生的成绩的众数为85,理科生成绩平均数为81,则x•y的值为( )