题目内容
5.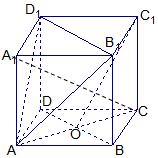 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证:
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证:(1)C1O∥面AB1D1;
(2)平面A1AC⊥面AB1D1.
分析 (1)连结A1C1,设A1C1∩B1D1=O1,连结AO1,证明OC1∥AO1,然后证明C1O∥面AB1D1.
(2)证明A1C⊥B1D1,A1C⊥AB1,推出A1C⊥面AB1D1,即可证明平面A1AC⊥面AB1D1.
解答 证明:(1)连结A1C1,设A1C1∩B1D1=O1,
连结AO1,因为ABCD-A1B1C1D1是正方体∴A1ACC1是平行四边形
∴AC∥A1C1且 AC=A1C1.
又O,O1分别是AC,A1C1的中点,∴O1C1∥AO且O1C1=AO,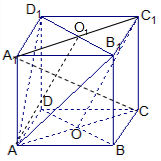
∴O1C1AO是平行四边形
∴OC1∥AO1,AO1?面AB1D1,O1C?面AB1D1
∴C1O∥面AB1D1.
(2)∵CC1⊥面A1B1C1D1,∴CC1⊥B1D1,
又∵A1C1⊥B1D1,∴B1D1⊥面A1C1C,
即A1C⊥B1D1,
同理可证A1C⊥AB1,
又AB1∩B1D1=B1,
∴A1C⊥面AB1D1,
∴平面A1AC⊥面AB1D1.
点评 本题考查直线与平面垂直,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
18.某质点运动的距离y与时间t的关系为y=t+lnt,那么这个质点在t=1时的瞬时速度为( )
| A. | e | B. | 2 | C. | 1 | D. | $\frac{1}{e}$ |
17.若变量x,y满足条$\left\{\begin{array}{l}y≥0\\ x+2y≥1\\ x+4y≤3\end{array}\right.$,则z=(x+1)2+y2的最小值是( )
| A. | 1 | B. | 2 | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{4}{5}$ |
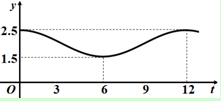 某企业一天中不同时刻的用电量y(万千瓦时)关于时间t(小时,0≤t≤24)的函数y=f(t)近似满足f(t)=Asin(ωt+φ)+B,(A>0,ω>0,0<φ<π).如图是函数y=f(t)的部分图象(t=0对应凌晨0点).
某企业一天中不同时刻的用电量y(万千瓦时)关于时间t(小时,0≤t≤24)的函数y=f(t)近似满足f(t)=Asin(ωt+φ)+B,(A>0,ω>0,0<φ<π).如图是函数y=f(t)的部分图象(t=0对应凌晨0点).