题目内容
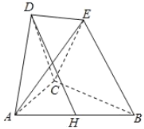
【题目】已知抛物线E:![]() 过点Q(1,2),F为其焦点,过F且不垂直于x轴的直线l交抛物线E于A,B两点,动点P满足△PAB的垂心为原点O.
过点Q(1,2),F为其焦点,过F且不垂直于x轴的直线l交抛物线E于A,B两点,动点P满足△PAB的垂心为原点O.
(1)求抛物线E的方程;
(2)求证:动点P在定直线m上,并求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)将点![]() 的坐标代入抛物线方程,由此求得
的坐标代入抛物线方程,由此求得![]() 的值,进而求得抛物线
的值,进而求得抛物线![]() 的方程.
的方程.
(2)设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程与抛物线的方程,写出韦达定理,设出直线
的方程与抛物线的方程,写出韦达定理,设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程求得
的方程求得![]() 的坐标,由此判断出动点
的坐标,由此判断出动点![]() 在定直线
在定直线![]() 上.求得
上.求得![]() 的表达式,利用基本不等式求得其最小值.
的表达式,利用基本不等式求得其最小值.
(1)将![]() 点坐标代入抛物线方程得
点坐标代入抛物线方程得![]() ,所以
,所以![]() .
.
(2)由(1)知抛物线![]() 的方程为
的方程为![]() ,所以
,所以![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,由
,由![]() 消去
消去![]() 得
得![]() ,所以
,所以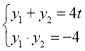 .由于
.由于![]() 为三角形
为三角形![]() 的垂心,所以
的垂心,所以 ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .同理可求得直线
.同理可求得直线![]() 的方程为
的方程为![]() .由
.由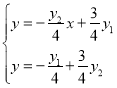 ,结合
,结合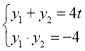 ,解得
,解得![]() ,所以
,所以![]() 在定直线
在定直线![]() 上.
上.
直线![]() 的方程为
的方程为![]() ,
,![]() 到直线
到直线![]() 的距离为
的距离为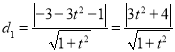 ,
,![]() 到直线
到直线![]() 的距离为
的距离为![]() .所以
.所以![]()
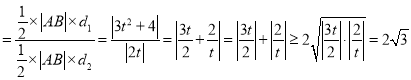 ,当且仅当
,当且仅当![]() 时取等号.所以
时取等号.所以![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目