ЬтФПФкШн
ЁОЬтФПЁПМКжЊдВF1ЃК(x+1)2 +y2= r2(1ЁмrЁм3)ЃЌдВF2ЃК(x-1)2+y2= (4-r)2ЃЎ
ЃЈ1ЃЉжЄУїЃКдВF1гыдВF2гаЙЋЙВЕуЃЌВЂЧѓЙЋЙВЕуЕФЙьМЃEЕФЗНГЬЃЛ
ЃЈ2ЃЉвбжЊЕуQ(mЃЌ0)(m<0)ЃЌЙ§ЕуEаБТЪЮЊk(kЁй0ЃЉЕФжБЯпгыЃЈЂёЃЉжаЙьМЃEЯрНЛгкMЃЌNСНЕуЃЌМЧжБЯпQMЕФаБТЪЮЊk1ЃЌжБЯпQNЕФаБТЪЮЊk2ЃЌЪЧЗёДцдкЪЕЪ§mЪЙЕУk(k1+k2)ЮЊЖЈжЕЃПШєДцдкЃЌЧѓГіmЕФжЕЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЌ![]() ЃЈ2ЃЉДцдкЃЌ
ЃЈ2ЃЉДцдкЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГідВ![]() КЭдВ
КЭдВ![]() ЕФдВаФКЭАыОЖЃЌЭЈЙ§дВF1гыдВF2гаЙЋЙВЕуЧѓГі
ЕФдВаФКЭАыОЖЃЌЭЈЙ§дВF1гыдВF2гаЙЋЙВЕуЧѓГі![]() ЕФЗЖЮЇЃЌДгЖјИљОн
ЕФЗЖЮЇЃЌДгЖјИљОн![]() ПЩЕУ
ПЩЕУ![]() ЕуЕФЙьМЃЃЌНјЖјЧѓГіЗНГЬЃЛ
ЕуЕФЙьМЃЃЌНјЖјЧѓГіЗНГЬЃЛ
ЃЈ2ЃЉЙ§![]() ЕуЧваБТЪЮЊ
ЕуЧваБТЪЮЊ![]() ЕФжБЯпЗНГЬЮЊ
ЕФжБЯпЗНГЬЮЊ![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЌСЊСЂжБЯпЗНГЬКЭЭждВЗНГЬЃЌИљОнЮЄДяЖЈРэвдМА
ЃЌСЊСЂжБЯпЗНГЬКЭЭждВЗНГЬЃЌИљОнЮЄДяЖЈРэвдМА![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌИљОнЦфЮЊЖЈжЕЃЌдђга
ЃЌИљОнЦфЮЊЖЈжЕЃЌдђга![]() ЃЌНјЖјПЩЕУНсЙћ.
ЃЌНјЖјПЩЕУНсЙћ.
ЃЈ1ЃЉвђЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
вђЮЊдВ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌдВ
ЃЌдВ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌ
ЃЌ
гжвђЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЫљвддВ![]() гыдВ
гыдВ![]() гаЙЋЙВЕуЃЌ
гаЙЋЙВЕуЃЌ
ЩшЙЋЙВЕуЮЊ![]() ЃЌвђДЫ
ЃЌвђДЫ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЕуЕФЙьМЃ
ЕуЕФЙьМЃ![]() ЪЧвд
ЪЧвд![]() ЃЌ
ЃЌ![]() ЮЊНЙЕуЕФЭждВЃЌ
ЮЊНЙЕуЕФЭждВЃЌ
Ыљвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
МДЙьМЃ![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§![]() ЕуЧваБТЪЮЊ
ЕуЧваБТЪЮЊ![]() ЕФжБЯпЗНГЬЮЊ
ЕФжБЯпЗНГЬЮЊ![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]()
гЩ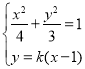 ЯћШЅ
ЯћШЅ![]() ЕУЕН
ЕУЕН![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ![]() ЃЌ Ђй
ЃЌ Ђй
вђЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ыљвд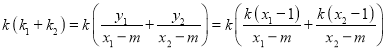
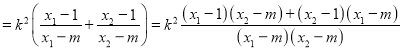
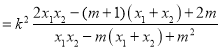 ЃЌ
ЃЌ
НЋЂйЪНДњШыећРэЕУ![]()
вђЮЊ![]() ЃЌ
ЃЌ
ЫљвдЕБ![]() ЪБЃЌМД
ЪБЃЌМД![]() ЪБЃЌ
ЪБЃЌ![]() .
.
МДДцдкЪЕЪ§![]() ЪЙЕУ
ЪЙЕУ![]() .
.

 КЫаФЫибјбЇСЗЦРЯЕСаД№АИ
КЫаФЫибјбЇСЗЦРЯЕСаД№АИ ЕЅдЊЦкжаЦкФЉОэЯЕСаД№АИ
ЕЅдЊЦкжаЦкФЉОэЯЕСаД№АИ