题目内容
以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,已知点M的极坐标是(2,θ),圆C的参数方程是
(t为参数),点M与圆C的位置关系是( )
|
| A、在圆内 | B、在圆上 |
| C、在圆外 | D、在圆上或圆外 |
考点:参数方程化成普通方程
专题:
分析:圆C的参数方程是
(t为参数),化为(x-1)2+y2=1.点M的极坐标是(2,θ),化为直角坐标.利用两点之间的距离得出点M到圆心C(1,0)的距离d与半径比较即可得出.
|
解答:
解:圆C的参数方程是
(t为参数),化为(x-1)2+y2=1.
点M的极坐标是(2,θ),其直角坐标为(2cosθ,2sinθ).
则点M到圆心C(1,0)的距离d=
=
∈[1,3].
因此点M在⊙C的外部或圆上.
故选:D.
|
点M的极坐标是(2,θ),其直角坐标为(2cosθ,2sinθ).
则点M到圆心C(1,0)的距离d=
| (2cosθ-1)2+(2sinθ)2 |
| 5-4cosθ |
因此点M在⊙C的外部或圆上.
故选:D.
点评:本题考查了把参数方程化为直角在暴风城、极坐标化为直角坐标、两点之间的距离公式、点与圆的位置关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
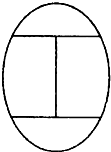 某校园有一椭圆型花坛,分成如图四块种花,现有4种不同颜色的花可供选择,要求每块地只能种一种颜色,且有公共边界的两块不能种同一种颜色,则不同的种植方法共有( )
某校园有一椭圆型花坛,分成如图四块种花,现有4种不同颜色的花可供选择,要求每块地只能种一种颜色,且有公共边界的两块不能种同一种颜色,则不同的种植方法共有( )| A、48种 | B、36种 |
| C、30种 | D、24种 |
执行如图所示的程序框图,输出的S是( )


| A、10 | B、15 | C、20 | D、35 |
已知双曲线
-
=1(a>0,b>0)的离心率为
,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
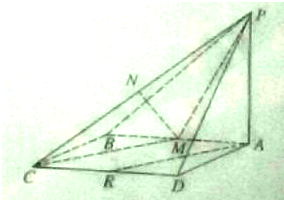 如图,已知矩形ABCD中,PA⊥平面ABCD,M,N,R分别是AB,PC,CD的中点,求证:
如图,已知矩形ABCD中,PA⊥平面ABCD,M,N,R分别是AB,PC,CD的中点,求证: