题目内容
12．已知空间直角坐标系中，A（1，-2，-1），B（3，0，1），则|AB|=（ ）| A． | 12 | B． | $2\sqrt{6}$ | C． | $2\sqrt{3}$ | D． | $\root{3}{12}$ |
分析 根据空间两点间的距离公式进行计算即可．
解答 解：∵A（1，-2，-1），B（3，0，1），
∴|AB|=$\sqrt{（1-3）^{2}+（-2）^{2}+（-1-1）^{2}}$=$\sqrt{4+4+4}$=2$\sqrt{3}$，
故选：C
点评 本题主要考查空间两点间的距离的计算，根据两点间的距离公式是解决本题的关键．
练习册系列答案
相关题目
14．若数列{an}是正项数列，且$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n}}$=n2+n，则a1+$\frac{{a}_{2}}{2}$+…+$\frac{{a}_{n}}{n}$等于（ ）
| A． | 2n2+2n | B． | n2+2n | C． | 2n2+n | D． | 2（n2+2n） |
17．
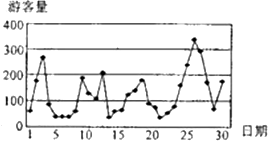已知云台山景区对拥挤等级与每日游客数量（单位：百人）的关系有如下规定：当n∈[0，100）时，拥挤等级为“优”；当n∈[100，200）时，拥挤等级为“良”；当n∈[200，300）时，拥挤等级为“拥挤”；当n≥300时，拥挤等级为“严重拥挤”．该景区对9月份的游客数量作出如图的统计数据．
（1）下面是根据统计数据得到的频率分布直方表，求出a，b，c的值，并估计该景区9月份游客人数的平均值（同一组中的数据用该组区间的中点值作代表）；
（2）某人选择在9月1日至9月5日这5天中任选2天到该景区游玩，求他这2天遇到的游客拥挤等级均为“优”的概率．
已知云台山景区对拥挤等级与每日游客数量（单位：百人）的关系有如下规定：当n∈[0，100）时，拥挤等级为“优”；当n∈[100，200）时，拥挤等级为“良”；当n∈[200，300）时，拥挤等级为“拥挤”；当n≥300时，拥挤等级为“严重拥挤”．该景区对9月份的游客数量作出如图的统计数据．（1）下面是根据统计数据得到的频率分布直方表，求出a，b，c的值，并估计该景区9月份游客人数的平均值（同一组中的数据用该组区间的中点值作代表）；
| 游客数量 （单位：百人） | [0，100） | [100，200） | [200，300） | [300，400） |
| 天数 | a | 10 | 4 | c |
| 频率 | b | $\frac{1}{3}$ | $\frac{2}{15}$ | $\frac{1}{30}$ |
2．下面中的两个变量，具有相关关系的是（ ）
| A． |  | B． |  | C． |  | D． |  |