题目内容
18.设i为虚数单位,a,b∈R,下列命题中:①(a+1)i是纯虚数;
②若a>b,则a+i>b+i;
③若(a2-1)+(a2+3a+2)i是纯虚数,则实数a=±1;
④2i2>3i2.其中,真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①a=1时,(a+1)i=0,不是纯虚数,即可判断出正误;
②复数a+i与b+i无法比较大小,即可判断出正误;
③若(a2-1)+(a2+3a+2)i是纯虚数,则$\left\{\begin{array}{l}{{a}^{2}-1=0}\\{{a}^{2}+3a+2≠0}\end{array}\right.$,解得实数a,即可判断出真假;
④由于2i2=-2,3i2=-3,即可判断出大小关系.
解答 解:①a=-1时,(a+1)i=0,不是纯虚数,是假命题;
②若a>b,但是a+i与b+i无法比较大小,是假命题;
③若(a2-1)+(a2+3a+2)i是纯虚数,则$\left\{\begin{array}{l}{{a}^{2}-1=0}\\{{a}^{2}+3a+2≠0}\end{array}\right.$,解得实数a=1,因此是假命题;
④∵i2=1,2i2=-2,3i2=-3,∴2i2>3i2,是真命题.
真命题的个数有1.
故选:A.
点评 本题考查了复数的运算法则及其有关知识,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
5.由点P向圆x2+y2=1引两条切线PA、PB,A、B是切点,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值是( )
| A. | 6-4$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 2$\sqrt{2}$-3 | D. | 4$\sqrt{2}$-6 |
 ,若当
,若当 时,
时, 取得极小值,则
取得极小值,则 ___________.
___________.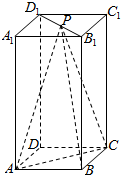 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,P为线段B1D1上一点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,P为线段B1D1上一点.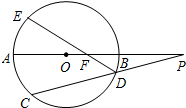 如图,圆O的直径AB的延长线与弦CD的延长线交于点P,E是圆O上的一点,弧$\widehat{AE}$与弧$\widehat{AC}$相等,ED与AB交于点F,AF>BF.
如图,圆O的直径AB的延长线与弦CD的延长线交于点P,E是圆O上的一点,弧$\widehat{AE}$与弧$\widehat{AC}$相等,ED与AB交于点F,AF>BF.