题目内容
13.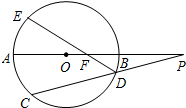 如图,圆O的直径AB的延长线与弦CD的延长线交于点P,E是圆O上的一点,弧$\widehat{AE}$与弧$\widehat{AC}$相等,ED与AB交于点F,AF>BF.
如图,圆O的直径AB的延长线与弦CD的延长线交于点P,E是圆O上的一点,弧$\widehat{AE}$与弧$\widehat{AC}$相等,ED与AB交于点F,AF>BF.(Ⅰ)若AB=11,EF=6,FD=4,求BF;
(Ⅱ)证明:PF?PO=PA?PB.
分析 (Ⅰ)连接OC,OE,由相交弦定理,得FA•FB=FE•FD,利用AF>BF,求BF;
(Ⅱ)利用割线定理,结合△PDF∽△POC,即可证明PF•PO=PA•PB.
解答 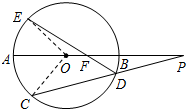 (Ⅰ)解:由相交弦定理,得FA•FB=FE•FD,(1分)
(Ⅰ)解:由相交弦定理,得FA•FB=FE•FD,(1分)
即(11-FB)•FB=6×4,(2分)
解得BF=3或BF=8,(3分)
因为AF>BF,所以BF=3.(4分)
(Ⅱ)证明:连接OC,OE.
因为弧AE等于弧AC,所以$∠AOC=∠AOE=\frac{1}{2}∠EOC=∠EDC$,(5分)
所以∠POC=∠PDF,(6分)
又∠P=∠P,所以△POC∽△PDF,(7分)
所以$\frac{PO}{PD}=\frac{PC}{PF}$,即PO•PF=PC•PD,(8分)
又因为PA•PB=PC•PD,(9分)
所以PF•PO=PA•PB.((10分)
点评 本题考查相交弦定理,考查割线定理,三角形相似的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.设i为虚数单位,a,b∈R,下列命题中:
①(a+1)i是纯虚数;
②若a>b,则a+i>b+i;
③若(a2-1)+(a2+3a+2)i是纯虚数,则实数a=±1;
④2i2>3i2.其中,真命题的个数有( )
①(a+1)i是纯虚数;
②若a>b,则a+i>b+i;
③若(a2-1)+(a2+3a+2)i是纯虚数,则实数a=±1;
④2i2>3i2.其中,真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.函数f(x)=2x-x2的零点所在的一个区间是( )
| A. | (-$\frac{1}{2}$,0) | B. | ($\frac{3}{2}$,$\frac{5}{2}$) | C. | ($\frac{9}{2}$,$\frac{11}{2}$) | D. | (4,+∞) |
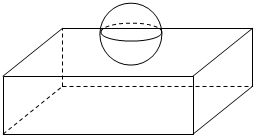 “80后文艺膏年小张在”祭我们逝去的青春“系列活动中,设计了一个与弹珠有关的玩具模型,它是由一个长方体和一个球焊接而成,如图所示,该几何体的球半径为R,其长方体的长和宽都是6R,高为$\frac{3}{2}$R:
“80后文艺膏年小张在”祭我们逝去的青春“系列活动中,设计了一个与弹珠有关的玩具模型,它是由一个长方体和一个球焊接而成,如图所示,该几何体的球半径为R,其长方体的长和宽都是6R,高为$\frac{3}{2}$R: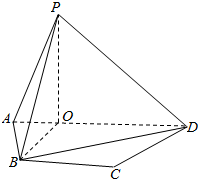 如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.
如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.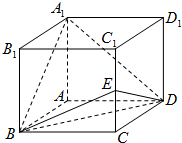 如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD为菱形,∠ABC=60°,E是CC1的中点,且A1B⊥A1D.
如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD为菱形,∠ABC=60°,E是CC1的中点,且A1B⊥A1D.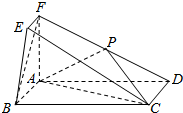 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.