题目内容
6.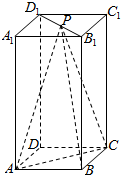 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,P为线段B1D1上一点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,P为线段B1D1上一点.(Ⅰ) 求证:AC⊥BP;
(Ⅱ) 当P为线段B1D1的中点时,求点A到平面PBC的距离.
分析 (Ⅰ)连结BD,证明AC⊥BD,AC⊥BB1,说明AC⊥平面BB1D1D,即可证明AC⊥BP.
(Ⅱ)求出VP-ABC,l设三棱锥A-PBC的高为h,利用VA-PBC=VP-ABC,即可求解三棱锥A-PBC的高.
解答 (本小题满分12分)
解:(Ⅰ)证明:连结BD,因为ABCD-A1B1C1D1是长方体,且AB=BC=2,
所以四边形ABCD是正方形,所以AC⊥BD,…(1分)
因为在长方体ABCD-A1B1C1D1中,BB1⊥平面ABCD,AC?平面ABCD,
所以AC⊥BB1,…(2分)
因为BD?平面BB1D1D,BB1?平面BB1D1D,
且BD∩BB1=B,…(3分)
所以AC⊥平面BB1D1D,…(4分)
因为BP?平面BB1D1D,所以AC⊥BP.…(5分)
(Ⅱ)点P到平面ABC的距离AA1=4,…(6分)△ABC的面积${S_{△ABC}}=\frac{1}{2}•AB•BC=2$,…(7分)
所以${V_{P-ABC}}=\frac{1}{3}{S_{△ABC}}•A{A_1}=\frac{1}{3}×2×4=\frac{8}{3}$,…(8分)
在Rt△BB1P中,$B{B_1}=4,{B_1}P=\sqrt{2}$,所以$BP=3\sqrt{2}$,同理$CP=3\sqrt{2}$.
又BC=2,所以△PBC的面积${S_{△PBC}}=\frac{1}{2}×2×\sqrt{{{({3\sqrt{2}})}^2}-{1^2}}=\sqrt{17}$.…(10分)
设三棱锥A-PBC的高为h,则因为VA-PBC=VP-ABC,所以$\frac{1}{3}{S_{△PBC}}•h=\frac{8}{3}$,…(11分)
所以$\frac{{\sqrt{17}}}{3}h=\frac{8}{3}$,解得$h=\frac{{8\sqrt{17}}}{17}$,即三棱锥A-PBC的高为$\frac{{8\sqrt{17}}}{17}$.…(12分)
点评 本题考查几何体的体积的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及转化思想的应用.

| A. | $\frac{π}{4}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{π}{3}$ |
①(a+1)i是纯虚数;
②若a>b,则a+i>b+i;
③若(a2-1)+(a2+3a+2)i是纯虚数,则实数a=±1;
④2i2>3i2.其中,真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“x∈R,x3-x2-1≤0”的否定是“?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$-1>0” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 函数y=1是幂函数 |
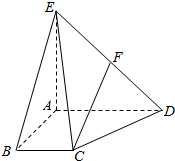 四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.
四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.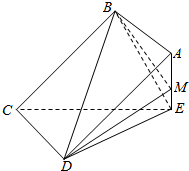 如图,矩形ABCD所在平面与三角形ECD所在平面相交于CD,AE⊥平面ECD
如图,矩形ABCD所在平面与三角形ECD所在平面相交于CD,AE⊥平面ECD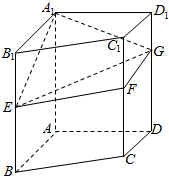 如图直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AB∥DC,∠BAD=90°,AA1=AB=2CD=4,AD=2,E、F、G分别是侧棱BB1、C1C、DD1上的点,BE=2,DG=3.
如图直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AB∥DC,∠BAD=90°,AA1=AB=2CD=4,AD=2,E、F、G分别是侧棱BB1、C1C、DD1上的点,BE=2,DG=3.